こんにちは、ひかりです。
今回は線形代数学からベクトルの長さと内積・外積について解説していきます。
ベクトルの定義と演算(和とスカラー倍)について知りたい方は、前回の記事をご覧ください。
この記事では以下のことを紹介します。
- ベクトルの長さの求め方とは?
- 始点が原点でないベクトルについて
- ベクトルの内積について
- ベクトルの外積について
ベクトルの長さ
前回の記事で、ベクトルは直線の矢印で表現できることを紹介しました。
ここでは、その矢印の(つまりベクトルの)長さを求めてみましょう。
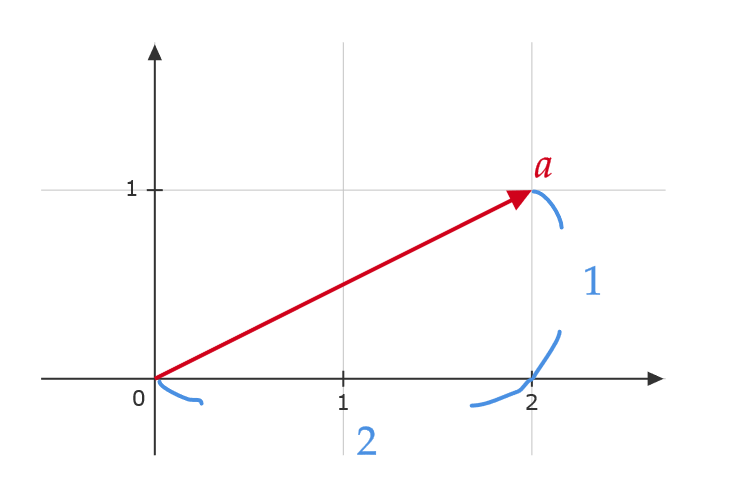
ベクトル \( \mathbf{a}=\begin{pmatrix} 2 \\ 1 \end{pmatrix} \) の長さを \( \| \mathbf{a} \| \) とおくと、これは三平方の定理より、
$$ \|\mathbf{a}\|=\sqrt{2^2+1^2}=\sqrt{5} $$
これを \( n \) 次元ベクトルに一般化します。
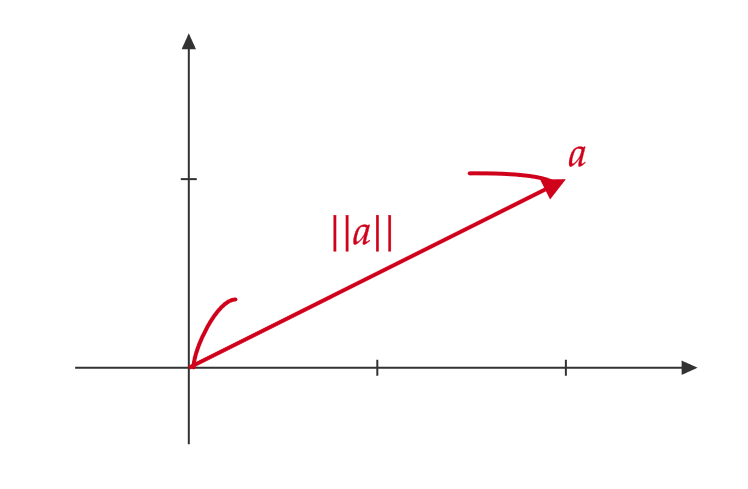
ベクトル \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} \) の長さを \( \|\mathbf{a}\| \) と表して、次のように計算されます。
$$ \|\mathbf{a}\|=\sqrt{a_1^2+a_2^2+\dots+a_n^2} $$
ここで、1つ特別なベクトルを紹介します。
長さが \( 1 \) であるベクトルを単位ベクトルといい、 \( \mathbf{e} \) などと表す。
つまり、 \( \|\mathbf{e}\|=1 \)
ゼロベクトルでないベクトル \( \mathbf{a} \) があったとして、そこから単位ベクトルを構成することができます。
具体的には、 \( \mathbf{e}=\frac{1}{\|\mathbf{a}\|}\mathbf{a} \) とおくと、これは \( \mathbf{a} \) と同じ向きの単位ベクトルとなります。
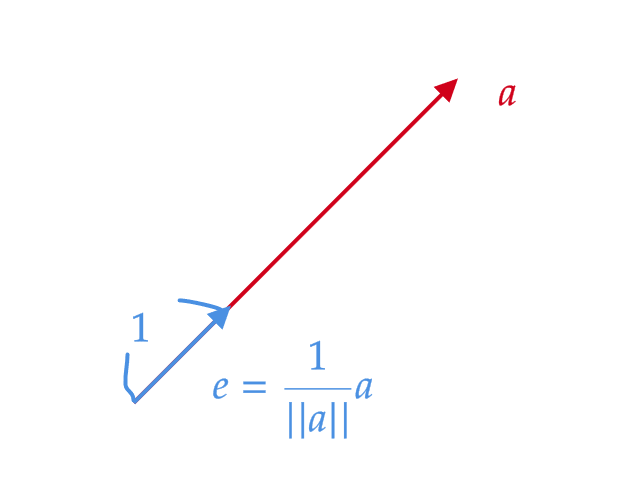
\( \mathbf{a}=\begin{pmatrix} 2 \\ 1 \end{pmatrix} \) と同じ向きの単位ベクトルは
$$ \mathbf{e}=\frac{1}{\|\mathbf{a}\|}\mathbf{a}=\frac{1}{\sqrt{5}}\begin{pmatrix} 2 \\ 1 \end{pmatrix}=\begin{pmatrix} \frac{2}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \end{pmatrix} $$
始点が原点でないベクトル
ここまでのベクトルはすべて原点 \( (0,0) \) を始点としたものを考えてきました。
ここでは、始点が原点でないベクトルについて考えていきます。
点 \( A=(a_1,a_2) \) を始点とし、点 \( B=(b_1,b_2) \) を終点とするベクトルを \( \overrightarrow{AB} \) と表します。
このベクトルは原点 \( O \) を通るまわり道で表すことができます。
\( \overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}. \)
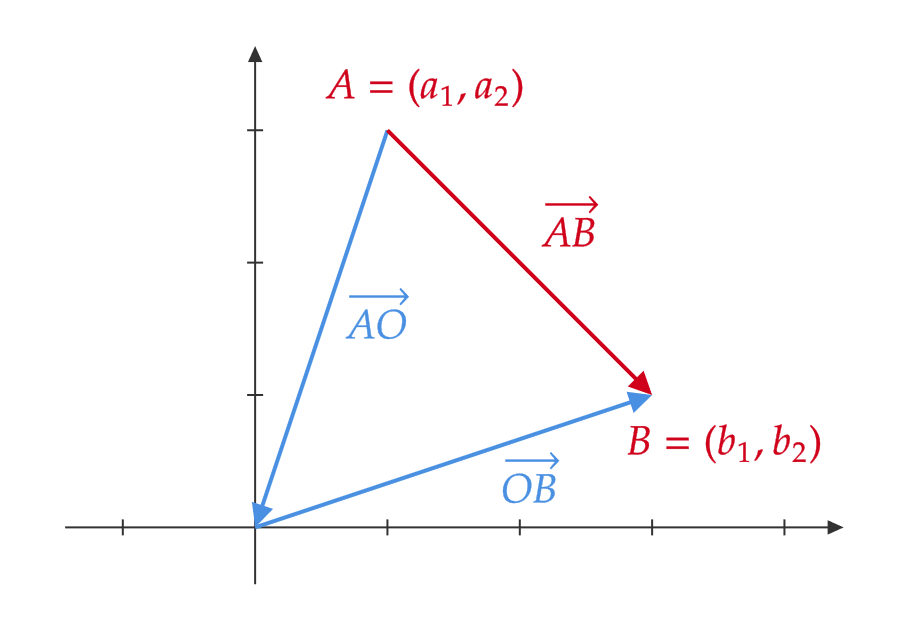
\( \overrightarrow{AO}=-\overrightarrow{OA} \) より、 \( \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA} \) となります。
よって、 \( \overrightarrow{OA}=\mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}, \ \overrightarrow{OB}=\mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \end{pmatrix} \) とおくと、
$$ \begin{align} \overrightarrow{AB}=\mathbf{b}-\mathbf{a}=\mathbf{b}+(-\mathbf{a})=\begin{pmatrix} b_1 \\ b_2 \end{pmatrix}+\begin{pmatrix} -a_1 \\ -a_2 \end{pmatrix}=\begin{pmatrix} b_1-a_1 \\b_2-a_2 \end{pmatrix} \end{align} $$
また、 \( \overrightarrow{AB} \) の大きさ \( \|\overrightarrow{AB}\| \) は、
$$ \|\overrightarrow{AB}\|=\|\mathbf{b}-\mathbf{a}\|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2} $$
と計算できます。
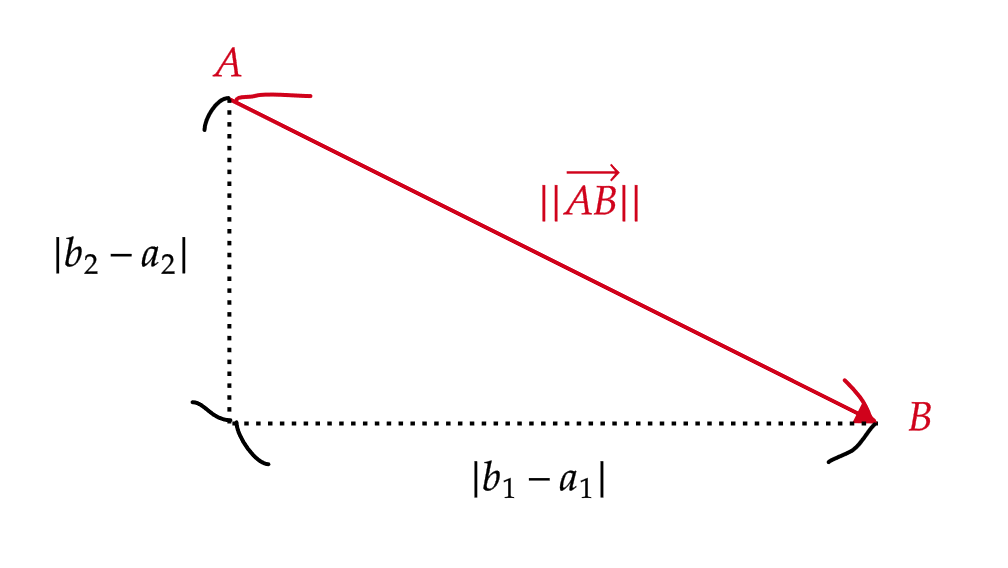
点 \( A=(3,-1) \) を始点、点 \( B=(-1,2) \) を終点とするベクトル \( \overrightarrow{AB} \) の大きさ \( \|\overrightarrow{AB}\| \) を求める。
\( \overrightarrow{OA}=\mathbf{a}=\begin{pmatrix} 3 \\ -1 \end{pmatrix}, \ \overrightarrow{OB}=\mathbf{b}=\begin{pmatrix} -1 \\ 2 \end{pmatrix} \) とおくと、
$$ \begin{align} \overrightarrow{AB}=\mathbf{b}-\mathbf{a}=\mathbf{b}+(-\mathbf{a})=\begin{pmatrix} -1 \\ 2 \end{pmatrix}+\begin{pmatrix} -3 \\ 1 \end{pmatrix}=\begin{pmatrix} -4 \\ 3 \end{pmatrix} \end{align} $$
よって、 $$ \|\overrightarrow{AB}\|=\sqrt{(-4)^2+3^2}=\sqrt{16+9}=\sqrt{25}=5 $$
ベクトルの内積
前回の記事でベクトルの和とスカラー倍を紹介しました。
このスカラー倍というのは、通常の数(実数)とベクトルとの掛け算でした。
今回はベクトルとベクトルとの掛け算(ベクトルの積)について紹介します。
ベクトルの積は2種類ありますので、まずは内積について解説していきます。
内積の定義その1(成分表示による定義)
まず、2つの \( n \) 次元ベクトル
$$ \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} $$
に対して、\( \mathbf{a} \) と \( \mathbf{b} \) の内積 \( \mathbf{a}\cdot\mathbf{b} \) を次で定義する。
$$ \mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+\dots+a_nb_n. $$
\( \mathbf{a}=\begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} \) のとき、 \( \mathbf{a}\cdot\mathbf{b} \) を求める。
$$ \mathbf{a}\cdot\mathbf{b}=1\times 2+(-1)\times 1+2\times 3=7 $$
内積の定義その2(長さとなす角による定義)
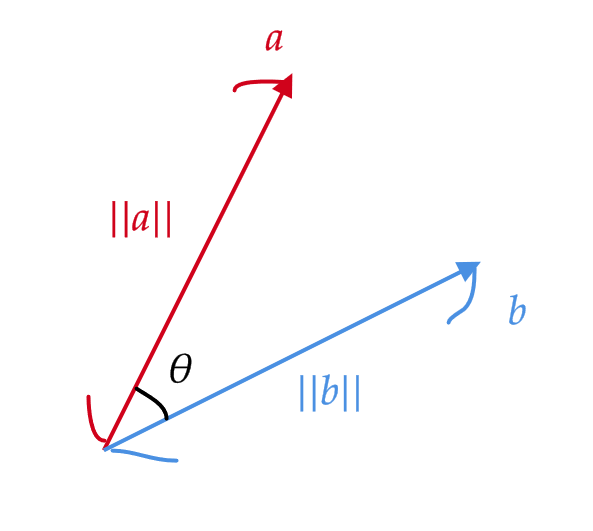
2つのベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の成分がわかっていなくても、2つのベクトルの長さ \( \|\mathbf{a}\|,\|\mathbf{b}\| \) とそのなす角 \( \theta \) によっても内積は定義できます。
2つのベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の長さ \( \|\mathbf{a}\|,\|\mathbf{b}\| \) とそのなす角 \( \theta \) に対して、 \( \mathbf{a} \) と \( \mathbf{b} \) の内積 \( \mathbf{a}\cdot\mathbf{b} \) を次で定義する。
$$ \mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta $$
(三角関数については、高校数学(数学Ⅲ)03の記事をご覧ください。)
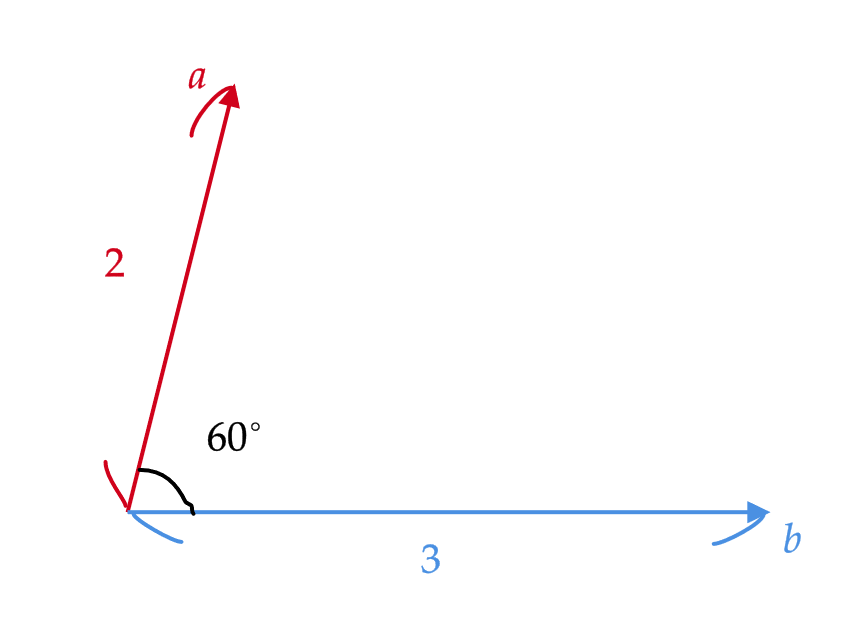
図のような2つのベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の内積 \( \mathbf{a}\cdot \mathbf{b} \) を求める。
$$ \mathbf{a}\cdot\mathbf{b}=2\times 3\times \cos 60^\circ=2\times 3\times \frac{1}{2}=3 $$
内積の図形的な意味
ベクトルの内積とは、いったい何を表しているのでしょうか。
そのため、2つのベクトル \( \mathbf{a},\mathbf{b} \) に対して、 \( \mathbf{b} \) を \( \mathbf{a} \) に向かって射影したものを考えます。
射影とは何かといいますと、図のようにベクトル \( \mathbf{a} \) を地面だと思い、その真上から太陽の光を当てたときにベクトル \( \mathbf{b} \) の影のことです。
この影の長さは \( \|\mathbf{b}\|\cos\theta \) で与えられます。
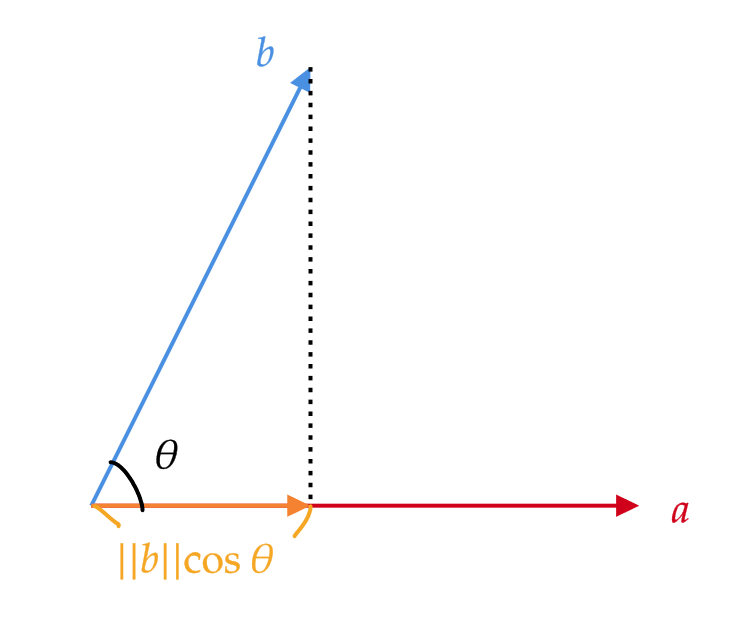
よって、定義4より、 \( \displaystyle \|\mathbf{b}\|\cos\theta=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{a}\|} \) となります。
まとめると、 \( \displaystyle \frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{a}\|} \) は \( \mathbf{b} \) を \( \mathbf{a} \) に向かって射影したものの長さとなります。
内積の性質
ベクトル \( \mathbf{a},\mathbf{b},\mathbf{c} \) と実数 \( k \) に対して、次が成り立つ。
(1) \( \mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{a} \)
(2) \( \mathbf{a}\cdot(\mathbf{b}+\mathbf{c})=\mathbf{a}\cdot\mathbf{b}+\mathbf{a}\cdot\mathbf{c} \)
(3) \( k\mathbf{a}\cdot\mathbf{b}=\mathbf{a}\cdot k\mathbf{b}=k(\mathbf{a}\cdot\mathbf{b}) \)
(4) \( \mathbf{a}\cdot\mathbf{a}≧ 0 \) (等号は \( \mathbf{a}=0 \) のときに限る)
(5) \( \mathbf{a}\cdot\mathbf{b}=0 \ (\mathbf{a},\mathbf{b}\not=0) \) のとき \( \mathbf{a} \) と \(\mathbf{b} \) は直交する。
定理1の証明(気になる方だけクリックしてください)
(1)と(5)を示していきます。
(1) \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} \) とおきます。このとき、
$$ \begin{align} \mathbf{a}\cdot\mathbf{b}&=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}\cdot\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}=a_1b_1+a_2b_2+\cdots+a_nb_n \\ &=b_1a_1+b_2a_2+\cdots+b_na_n=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}\cdot\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}=\mathbf{b}\cdot\mathbf{a} \end{align} $$
(5) \( \mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta \) であるので、 \( \mathbf{a}\cdot\mathbf{b}=0 \) であるならば、 \( \|\mathbf{a}\|\|\mathbf{b}\|\cos\theta=0 \) となります。
いま、\( \mathbf{a},\mathbf{b}\not=0 \) であるので、 \( \|\mathbf{a}\|,\|\mathbf{b}\|\not=0 \) となります。
よって、 \( \cos\theta=0 \) となるので、 \( \theta=90^{\circ},270^{\circ} \) となります。
したがって、 \( \mathbf{a} \) と \( \mathbf{b} \) は直交します。
ベクトルの外積
次に、ベクトルの2つ目の積である外積について紹介します。
まず、前提としてベクトルの外積は3次元ベクトルのみ定義することができます。
それ以外の次元では外積は考えることができないことに注意してください。
外積の定義
2つの \( 3 \) 次元ベクトル \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \) に対して、\( \mathbf{a} \) と \( \mathbf{b} \) の外積 \( \mathbf{a}\times\mathbf{b} \) を次で定義します。
$$ \mathbf{a}\times\mathbf{b}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}\times\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}=\begin{pmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{pmatrix}. $$
\( \mathbf{a}=\begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} \) のとき、 \( \mathbf{a}\times\mathbf{b} \) を求める。
$$ \mathbf{a}\times\mathbf{b}=\begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix}\times\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}=\begin{pmatrix} (-1)\times 3-2\times 1 \\ 2\times 2-1\times 3 \\ 1\times 1-(-1)\times 2 \end{pmatrix}=\begin{pmatrix} -5 \\ 1 \\ 3 \end{pmatrix}. $$
外積の図形的な意味
ベクトルの外積とは、いったい何を表しているのでしょうか。
2つの3次元ベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の外積 \( \mathbf{a}\times \mathbf{b} \) とは次の2つの条件をみたす新しいベクトルとなります。
(1) \( \mathbf{a} \) と \( \mathbf{b} \) 両方に直交する。(ただし、向きは \( \mathbf{a} \) から \( \mathbf{b} \) へ回転する右ねじの方向)
(2) ベクトル \( \mathbf{a}\times\mathbf{b} \) の長さは \( \mathbf{a} \) と \( \mathbf{b} \) で作られる平行四辺形の面積と等しい。
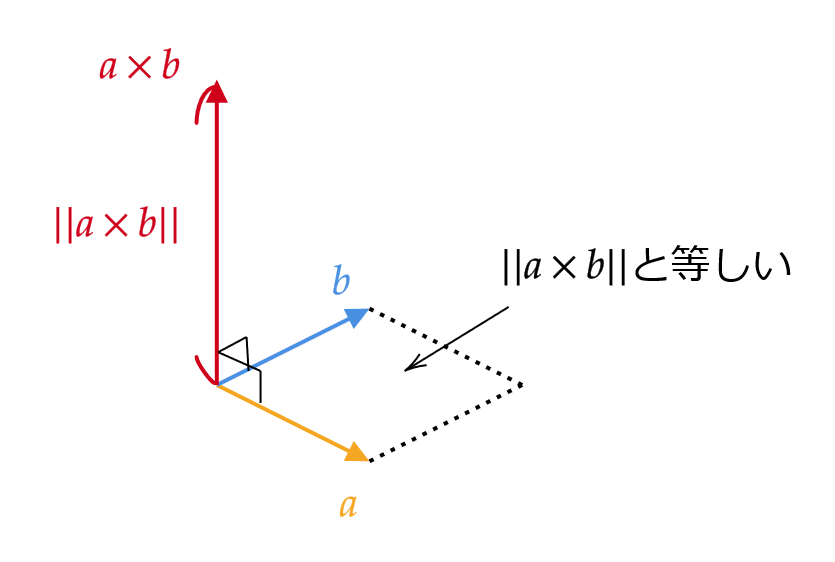
外積の性質
ベクトル \( \mathbf{a},\mathbf{b},\mathbf{c} \) と実数 \( k \) に対して、次が成り立つ。
(1) \( \mathbf{a}\times\mathbf{b}=-\mathbf{b}\times\mathbf{a} \) (マイナスがつくことに注意)
(2) \( \mathbf{a}\times(\mathbf{b}+\mathbf{c})=\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c} \)
(3) \( k\mathbf{a}\times\mathbf{b}=\mathbf{a}\times k\mathbf{b}=k(\mathbf{a}\times\mathbf{b}) \)
(4) \( \mathbf{a}\times\mathbf{a}=0 \)
(5) \( (\mathbf{a}\times\mathbf{b})\cdot \mathbf{a}=(\mathbf{a}\times\mathbf{b})\cdot \mathbf{b}=0 \) (つまり \( \mathbf{a}\times\mathbf{b} \) は \(\mathbf{a} \) と \(\mathbf{b} \) 両方に直交する)
(6) \( \|\mathbf{a}\times\mathbf{b}\|=\|\mathbf{a}\|\|\mathbf{b}\|\sin\theta \quad (\text{ただし} \ \theta \ \text{は} 0\le \theta \le \pi \ \text{となるように選ぶ}) \)
(つまり \( \mathbf{a}\times\mathbf{b} \) の長さは \( \mathbf{a} \) と \(\mathbf{b} \) から作られる平行四辺形の面積)
定理2の証明(気になる方だけクリックしてください)
(1)と(6)を示していきます。
(1) \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \) とおきます。このとき、
$$ \begin{align} \mathbf{a}\times\mathbf{b}&=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}\times\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}=\begin{pmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{pmatrix} \\ &=\begin{pmatrix} -(a_3b_2-a_2b_3) \\ -(a_1b_3-a_3b_1) \\ -(a_2b_1-a_1b_2) \end{pmatrix}=\begin{pmatrix} -(b_2a_3-b_3a_2) \\ -(b_3a_1-b_1a_3) \\ -(b_1a_2-b_2a_1) \end{pmatrix} \\ &=-\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}\times\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}=-\mathbf{b}\times\mathbf{a} \end{align} $$
(6) \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \) とおきます。まず、
$$ \begin{align} \|\mathbf{a}\times\mathbf{b}\|^2&=\left\|\begin{pmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{pmatrix}\right\|^2 \\ &=(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2 \\ &=a_2^2b_3^2+a_3^2b_2^2+a_3^2b_1^2+a_1^2b_3^2+a_1^2b_2^2+a_2^2b_1^2 \\ & \qquad -2(a_2a_3b_2b_3+a_1a_3b_1b_3+a_1a_2b_1b_2) \end{align} $$
一方で、
$$ \begin{align} \|\mathbf{a}\|^2\|\mathbf{b}\|^2\sin^2\theta&=\|\mathbf{a}\|^2\|\mathbf{b}\|^2(1-\cos^2\theta)=\|\mathbf{a}\|^2\|\mathbf{b}\|^2-(\mathbf{a}\cdot\mathbf{b})^2 \\ &=(a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2)-(a_1b_1+a_2b_2+a_3b_3) \\ &=a_1^2b_2^2+a_1^2b_3^2+a_2^2b_1^2+a_2^2b_3^2+a_3^2b_1^2+a_3^2b_2^2 \\ & \qquad -2(a_1a_2b_1b_2+a_2a_3b_2b_3+a_1a_3b_1b_3) \end{align} $$
したがって、 \( \|\mathbf{a}\times\mathbf{b}\|^2=\|\mathbf{a}\|^2\|\mathbf{b}\|^2\sin^2\theta \)
ここで、 \( 0≦ \theta ≦ \pi \) であるので、 \( \sin\theta≧0 \) となります。
よって、 \( \|\mathbf{a}\times\mathbf{b}\|=\|\mathbf{a}\|\|\mathbf{b}\|\sin\theta \)
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

