こんにちは、ひかりです。
今回は複素関数論からローラン展開について解説していきます。
この記事では以下のことを紹介します。
- 孤立特異点とローラン展開可能性について
- ローラン展開の計算例について
孤立特異点とローラン展開可能性
複素関数論12の記事にて、複素関数の正則な点 \( a\in D \) を中心とするテイラー展開について紹介しました。
今回は複素関数の孤立特異点を中心とする展開について考えていきましょう。
まず、孤立特異点を次で定めます。
\( D\subset \mathbb{C} \) を領域、 \( a\in D, \) \( f:D\backslash\{a\}\to \mathbb{C} \) とする。
このとき、 \( f \) が \( a \) で微分可能でないとき、 \( a \) を \( f \) の特異点という。
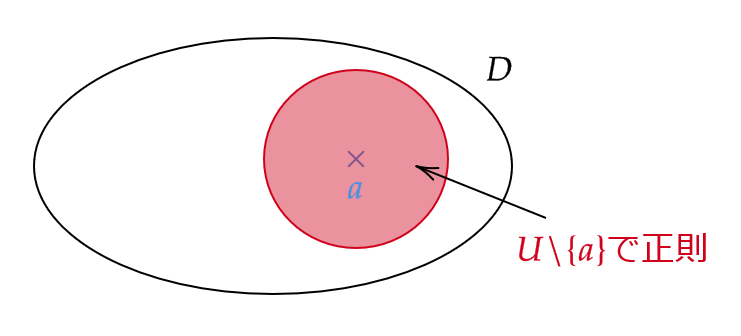
また、 \( a \) が \( f \) の特異点でかつ、ある \( a \) の近傍 \( U \) が存在して \( f \) は \( U\backslash\{a\} \) 上正則であるとき、 \( a \) を \( f \) の孤立特異点という。
そして、孤立特異点 \( a \) を中心とする展開であるローラン展開を定義します。
\( D\subset \mathbb{C} \) を領域、 \( a\in D \) として、 \( f:D\backslash\{a\}\to \mathbb{C} \) を \( D\backslash\{a\} \) 上正則とする。
このとき、孤立特異点 \( a \) を中心とする \( f \) のローラン展開を次で定める。
\[ f(z)=\sum_{n=-\infty}^{\infty}c_n(z-a)^n \]
このとき、ローラン展開可能性について次のことが成り立ちます。
\( D\subset \mathbb{C} \) を領域、 \( a\in D \) として、 \( f:D\backslash\{a\}\to \mathbb{C} \) を \( D\backslash\{a\} \) 上正則とする。
このとき、 \( a \) の近傍 \( U \) において \( f \) は次のようにローラン展開可能である。
\[ f(z)=\sum_{n=-\infty}^{\infty}\left( \frac{1}{2\pi i}\int_{C_0}\frac{f(\zeta)}{(\zeta-a)^{n+1}}d\zeta \right) (z-a)^n \]
ここで、 \( C_0 \) は \( a \) を中心とする \( D \) 内の円である。
定理1の証明(気になる方だけクリックしてください)
もう少しお待ちください。
ローラン展開の計算例
それでは、実際にローラン展開の例を見ていきましょう。
\( \frac{1}{(z-1)(z-2)} \) の \( z=1 \) を中心とするローラン展開を求める。
\[ \begin{align} \frac{1}{(z-1)(z-2)}&=\frac{1}{z-1}\frac{1}{z-2}=\frac{1}{z-1}\frac{1}{-1+(z-1)}=\frac{1}{z-1}\frac{-1}{1-(z-1)} \\ &=\frac{1}{z-1}\left(-\sum_{n=0}^{\infty}(z-1)^n \right)=-\sum_{n=-1}^{\infty}(z-1)^n \end{align} \]
したがって、 \( \frac{1}{(z-1)(z-2)} \) の \( z=1 \) を中心とするローラン展開は
\[ \frac{1}{(z-1)(z-2)}=-\sum_{n=-1}^{\infty}(z-1)^n \]
\( z^2e^{-\frac{1}{z}} \) の \( z=0 \) を中心とするローラン展開を求める。
\[ \begin{align} z^2e^{-\frac{1}{z}}&=z^2\sum_{n=0}^{\infty}\frac{1}{n!}\left(-\frac{1}{z}\right)^n=\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}z^{2-n} \\ &=z^2-z+\frac{1}{2!}z^0-\frac{1}{3!}z^{-1}+\frac{1}{4!}z^{-2}-\cdots=\sum_{n=-\infty}^2\frac{(-1)^n}{(2-n)!}z^n \end{align} \]
したがって、 \( z^2e^{-\frac{1}{z}} \) の \( z=0 \) を中心とするローラン展開は
\[ z^2e^{-\frac{1}{z}}=\sum_{n=-\infty}^2\frac{(-1)^n}{(2-n)!}z^n \]
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

