こんにちは、ひかりです。
今回は曲線・曲面論から大域的なガウス・ボンネの定理について解説していきます。
この記事では以下のことを紹介します。
- 閉曲面のオイラー数について
- 大域的なガウス・ボンネの定理について
閉曲面のオイラー数
ここでは、大域的なガウス・ボンネの定理の準備として、閉曲面のオイラー数について考えます。
まず境界のない曲面のことを閉曲面といいます。
そして、裏と表が区別できる閉曲面を向き付け可能な曲面といいます。
この向き付け可能な閉曲面に対してオイラー数を次のように定義します。
\( S \) を向き付け可能な閉曲面とする。
また、 \( S \) を三角形分割をしたときの頂点、辺、面の個数の総和をそれぞれ \( b_0,b_1,b_2 \) とする。
このとき、 \( \chi(s)=b_0-b_1+b_2 \) とおいて、 \( S \) のオイラー数という。
(1) 球面を下のように分割をする。
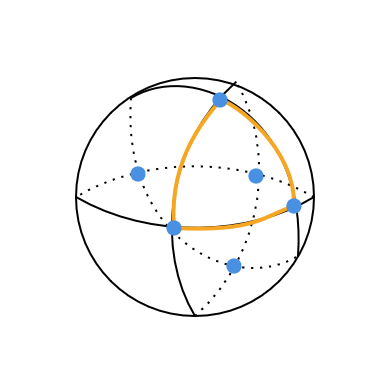
このとき、 \( b_0=6, \ b_1=12, \ b_2=8 \) であるので、
\[ \chi(球面)=6-12+8=2 \]
(2) 輪環面を下のように分割をする。
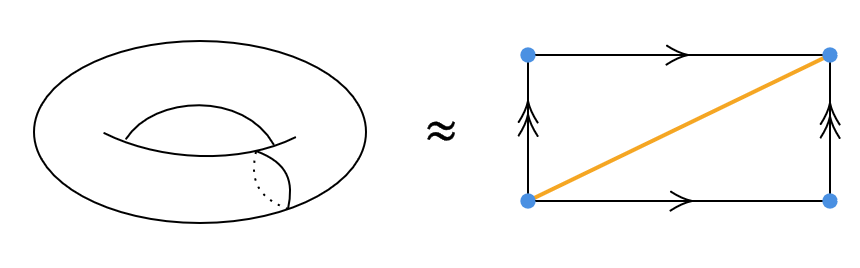
このとき、 \( b_0=1, \ b_1=3, \ b_2=2 \) であるので、
\[ \chi(輪環面)=1-3+2=0 \]
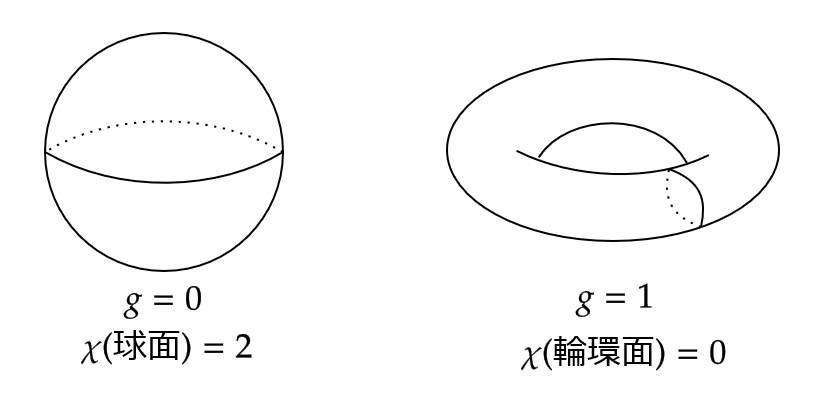
閉曲面の穴の数を種数といい、 \( g \) と表します。
このとき、 \( \chi(s)=2-2g \) であることが知られています。
大域的なガウス・ボンネの定理
それでは大域的なガウス・ボンネの定理を示しましょう。
\( S \) を向き付け可能な閉曲面として、ガウス曲率を \( \kappa \) とすると、
\[ \iint_D\kappa dS=2\pi \chi(s) \]
ここで、
\[ S=\bigcup_{j=1}^{b_2}\{\mathbf{p}(u,v) : (u,v)\in \Delta_j\} : 三角形分割, \quad D=\bigcup_{j=1}^{b_2}\Delta_j \]
定理1の証明(気になる方だけクリックしてください)
もう少しお待ちください。
半径 \( r \) の球面に対して、ガウス・ボンネの定理を確かめる。
\( \kappa=\frac{1}{r^2} \) であるので、
\[ \iint_D\kappa dS=\frac{1}{r^2}\iint_DdS=\frac{1}{r^2}\times 4\pi r^2=4\pi=2\pi \chi(球面) \]
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

