こんにちは、ひかりです。
今回は曲線・曲面論から局所的なガウス・ボンネの定理について解説していきます。
この記事では以下のことを紹介します。
- 閉曲線の回転数について
- 局所的なガウス・ボンネの定理について
閉曲線の回転数
ここでは、閉曲線の回転数について考えていきます。
まず、平面曲線を弧長パラメータ \( s \) を用いて
\[ \{\mathbf{p}(s) : s\in[a,b] \} \]
と表示します。ここで、 \( \mathbf{p} \) は位置ベクトルです。
このとき、 \( \mathbf{p}(a)=\mathbf{p}(b) \) をみたすとき、閉曲線といいます。
平面閉曲線
\[ \{\mathbf{p}(s) : s\in[a,b], \ \mathbf{p}\in C^2, \ \mathbf{p}(a)=\mathbf{p}(b), \ \mathbf{p}'(a)=\mathbf{p}'(b), \ \mathbf{p}^{\prime\prime}(a)=\mathbf{p}^{\prime\prime}(b)\} \]
に対して、ある整数 \( m\in \mathbb{Z} \) が存在して、次をみたす。
\[ \int_a^b\kappa(s)ds=2\pi m \]
ここで、 \( \kappa(s) \) はこの平面閉曲線の曲率である。
また、この \( m \) のことをこの平面閉曲線の回転数という。
定理1の証明(気になる方だけクリックしてください)
もう少しお待ちください。
半径 \( r \) の円(向きは反時計回り)の曲率は \( \frac{1}{r} \) であった。よって、
\[ \int_0^{2\pi r}\kappa(s)ds=\int_0^{2\pi r}\frac{1}{r}ds=2\pi \]
また以下の図は、回転数とその平面曲線のイメージを表したものである。
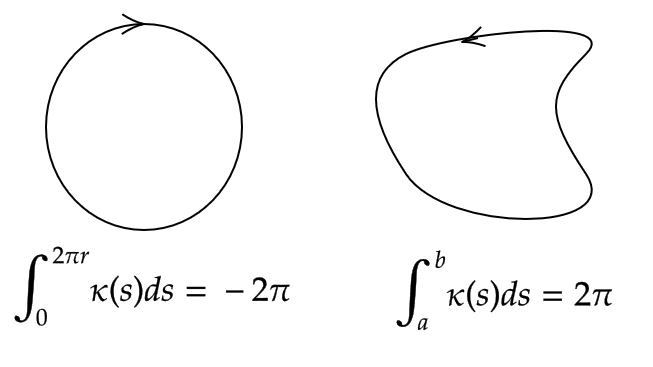
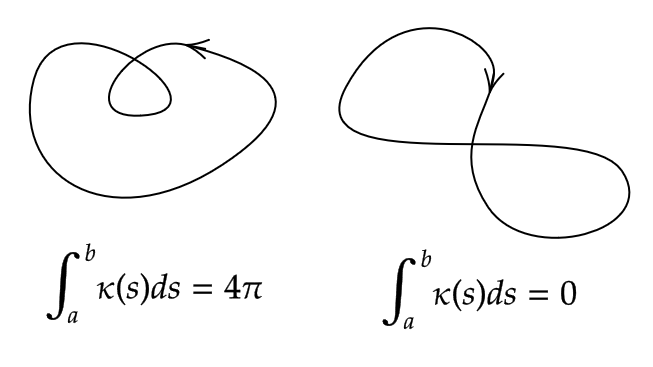
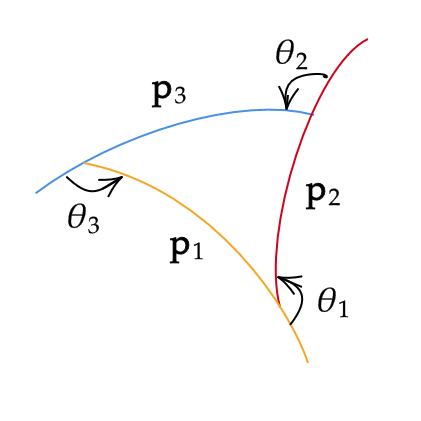
3つの \( C^2\)-級曲線 \( \mathbf{p}_i(s) \) (ただし、 \( a_i≦s≦b_i \) 、弧長パラメータ、 \( i=1,2,3 \)) で囲まれた図形を考える。
ここで、「囲まれた」というのは \( \mathbf{p}_i(b_i)=\mathbf{p}_{i+1}(a_{i+1}) \) を意味する。(ただし、 \( \mathbf{p}_4 \) は \( \mathbf{p}_1 \) と解釈する)
\( \mathbf{p}’_i(b_i) \) と \( \mathbf{p}’_{i+1}(a_{i+1}) \) のなす角(外角)を反時計回りに計ったものを \( \theta_i \) とする。
また、曲線 \( \mathbf{p}_i \) の曲率を \( \kappa^i \) とおく。このとき、次が成り立つ。
\[ \sum_{i=1}^3\left( \int_{a_i}^{b_i}\kappa^i ds+\theta_i \right)=2\pi \]
定理2の証明(気になる方だけクリックしてください)
もう少しお待ちください。
定理2を用いることにより、次のあたりまえの事実を示すことができます。
三角形の外角の和は \( 2\pi \) である。
定理3の証明(気になる方だけクリックしてください)
もう少しお待ちください。
局所的なガウス・ボンネの定理
まず、測地的曲率というものを定義します。
曲面 \( S \) を \( S=\{\mathbf{p}(u,v) : (u,v)\in D \} \) とする。
また、 \( \mathbf{c}=\mathbf{c}(s) \) を \( S \) 上の曲線(空間曲線)とする。
ここで、 \( s \) は弧長パラメータとする。
そして、 \( \mathbf{e}_1=\mathbf{c}'(s) \)、
\[ \mathbf{e}_2=「\mathbf{c}(s)\in Sにおける接平面上で、\mathbf{e}_1(s)を反時計回りに\frac{\pi}{2}回転したもの、 \]
\( \mathbf{e}_3(s)=\mathbf{e}_1(s)\times \mathbf{e}_2(s) \) とする。
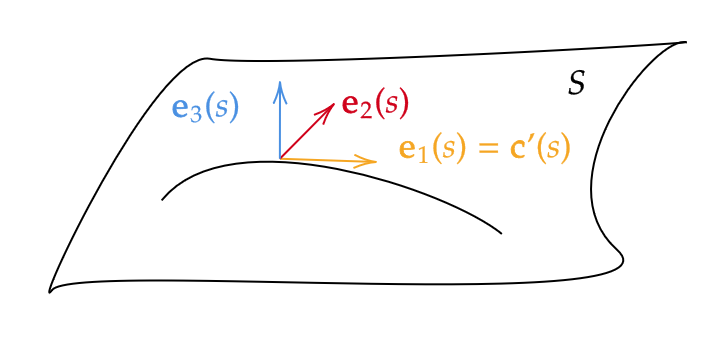
このとき、 \( \kappa_g(s)=\mathbf{c}^{\prime\prime}(s)\cdot \mathbf{e}_2(s) \) を \( S \) における \( \mathbf{c} \) の測地的曲率という。
また、 \( \kappa_n(s)=\mathbf{c}^{\prime\prime}(s)\cdot \mathbf{e}_3(s) \) を \( S \) における \( \mathbf{c} \) の法曲率という。
これをもとに、ガウス曲率の積分と測地的曲率の間に成り立つ等式について表した局所的なガウス・ボンネの定理を見ていきましょう。
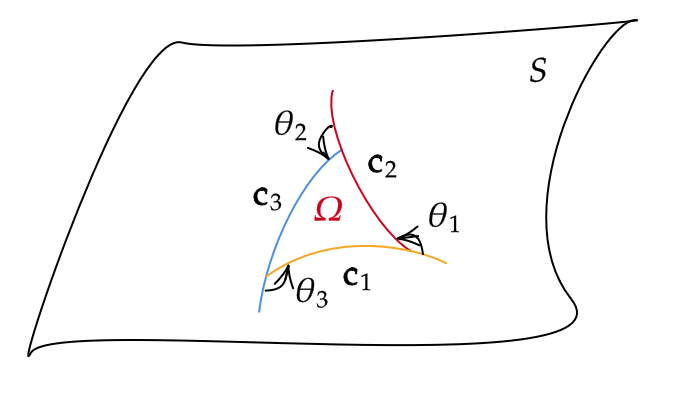
曲面 \( S \) 上に下図のような領域
\[ \Omega=\{\mathbf{p}(u,v) : (u,v)\in \Delta (\subset S)\} \]
を考える。また、 \( \kappa \) を \( S \) のガウス曲率、 \( \kappa_g^i \) を曲線 \( \mathbf{c}_i \) の測地的曲率とする。
そして、 \( dS=\sqrt{EG-F^2}dudv \) とおく。このとき、次が成り立つ。
\[ \iint_{\Delta}\kappa dS+\sum_{i=1}^3\left( \int_{a_i}^{b_i}\kappa_g^ids+\theta_i\right) =2\pi \]
定理4の証明(気になる方だけクリックしてください)
もう少しお待ちください。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

