こんにちは、ひかりです。
今回は複素関数論からコーシーの積分公式について解説していきます。
この記事では以下のことを紹介します。
- コーシーの積分公式について
- \( n \) 階微分に関するコーシーの積分公式について
コーシーの積分公式について
複素関数論08の記事にて、コーシーの積分定理を紹介しました。
これを用いて、 \( D\subset \mathbb{C} \) 上の正則関数 \( f \) の点 \( a\in D \) での値 \( f(a) \) がそのまわりの値によって決まってしまうというコーシーの積分公式を示すことができます。
\( D\subset \mathbb{C} \) を領域として、 \( f:D\to \mathbb{C} \) を \( D \) 上正則とする。
また、 \( a\in D \) として、
\[ D_R(a)=\{z\in \mathbb{C} : |z-a|<R\}\subset D \]
となる \( R>0 \) をとる。このとき、
\[ f(a)=\frac{1}{2\pi i}\int_{|z-a|=R}\frac{f(z)}{z-a}dz \]
定理1の証明(気になる方だけクリックしてください)
もう少しお待ちください。
\( C \) を以下の図のような閉曲線とするとき、 \( \displaystyle \int_C\frac{dz}{1+z^4} \) を求める。
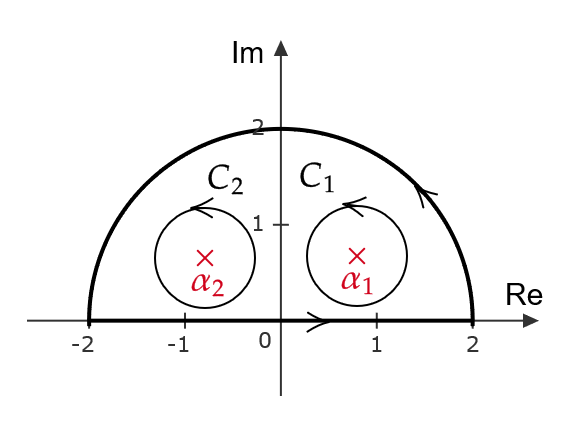
\[ \alpha_1=e^{\frac{\pi}{4}i}, \quad \alpha_2=e^{\frac{3}{4}\pi i}, \quad \alpha_3=e^{\frac{5}{4}\pi i}, \quad \alpha_4=e^{\frac{7}{4}\pi i} \]
とおくと、
\[ 1+z^4=(z-\alpha_1)(z-\alpha_2)(z-\alpha_3)(z-\alpha_4) \]
と因数分解できて、 \( \alpha_1,\alpha_2 \) は \( C \) の内側にある。
\( C_1,C_2 \) をそれぞれ \( \alpha_1,\alpha_2 \) 中心、半径 \( \frac{\sqrt{2}}{4} \) の円とすると、コーシーの積分定理より、
\[ \int_C\frac{dz}{1+z^4}=\int_{C_1}\frac{dz}{1+z^4}+\int_{C_2}\frac{dz}{1+z^4} \]
まず、
\[ \int_{C_1}\frac{dz}{1+z^4}=\int_{C_1}\frac{\frac{1}{(z-\alpha_2)(z-\alpha_3)(z-\alpha_4)}}{z-\alpha_1} \]
とかくと、 \( \frac{1}{(z-\alpha_2)(z-\alpha_3)(z-\alpha_4)} \) は \( C_1 \) の内側で正則なので、コーシーの積分公式より、
\[ \int_{C_1}\frac{dz}{1+z^4}=2\pi i\left( \frac{1}{(\alpha_1-\alpha_2)(\alpha_1-\alpha_3)(\alpha_1-\alpha_4)} \right)=\frac{\sqrt{2}}{4}\pi (1-i) \]
また、
\[ \int_{C_2}\frac{dz}{1+z^4}=\int_{C_2}\frac{\frac{1}{(z-\alpha_1)(z-\alpha_3)(z-\alpha_4)}}{z-\alpha_2} \]
とかくと、 \( \frac{1}{(z-\alpha_1)(z-\alpha_3)(z-\alpha_4)} \) は \( C_2 \) の内側で正則なので、コーシーの積分公式より、
\[ \int_{C_2}\frac{dz}{1+z^4}=2\pi i\left( \frac{1}{(\alpha_2-\alpha_1)(\alpha_2-\alpha_3)(\alpha_2-\alpha_4)} \right)=\frac{\sqrt{2}}{4}\pi (1+i) \]
したがって、
\[ \int_C\frac{dz}{1+z^4}=\frac{\sqrt{2}}{4}\pi (1-i)+\frac{\sqrt{2}}{4}\pi (1+i)=\frac{\sqrt{2}}{2}\pi \]
\( n \) 階微分に関するコーシーの積分公式について
定理1を繰り返し用いることにより、 \( n \) 階微分に関するコーシーの積分公式を示すことができます。
これにより、複素関数論03の定理1である正則関数が無限回微分可能であることが示されることになります。
\( D\subset \mathbb{C} \) を領域として、 \( f:D\to \mathbb{C} \) を \( D \) 上正則、 \( a\in D \) とする。
このとき、 \( f \) は無限回微分可能であり、 \( n\in\mathbb{N} \) と \( D_R(a)\subset D \) をみたす \( R>0 \) に対して、
\[ f^{(n)}(a)=\frac{n!}{2\pi i}\int_{|z-a|=R}\frac{f(z)}{(z-a)^{n+1}}dz \]
定理2の証明(気になる方だけクリックしてください)
もう少しお待ちください。
(1) \( \displaystyle \int_{|z-1|=1}\frac{5z^2-3z+2}{(z-1)^3}dz \) を求める。
\( 5z^2-3z+2 \) は \( \mathbb{C} \) 上正則であるので、コーシーの積分公式より、
$$ \begin{align*} \int_{|z-1|=1}\frac{5z^2-3z+2}{(z-1)^3}dz&=\frac{2\pi i}{2!}(5z^2-3z+2)^{\prime\prime}|_{z=1} \\ &=10\pi i \end{align*} $$
(2) \( \displaystyle \int_{|z|=1}\frac{\sin z}{z^4}dz \) を求める。
\( \sin z \) は \( \mathbb{C} \) 上正則であるので、コーシーの積分公式より、
$$ \begin{align*} \int_{|z|=1}\frac{\sin z}{z^4}dz&=\frac{2\pi i}{3!}(\sin z)^{\prime\prime\prime}|_{z=0} \\ &=-\frac{1}{3}\pi i \end{align*} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

