こんにちは、ひかりです。
今回は複素関数論から複素積分の定義とその性質について解説していきます。
この記事では以下のことを紹介します。
- 複素積分の定義とその性質について
複素積分の定義とその性質
まず、複素積分を定義するための準備として次を定義します。
(1) 集合 \( S \) の任意の2点が \( S \) 内にある連続曲線で結べるとき、 \( S \) は弧状連結であるという。
(2) 開集合かつ弧状連結な集合 \( D\subset \mathbb{C} \) を領域という。
これを用いて、複素積分を次のように定めます。
領域 \( D\subset \mathbb{C} \) 上の連続関数 \( f:D\to \mathbb{C} \) と \( D \) 内の曲線 \( C:\varphi(t) \ (a≦t≦b) \) に対して、 \( f \) の \( C \) に沿っての複素積分 \( \displaystyle \int_cf(z)dz \) を次で定める。
\[ \int_Cf(z)dz=\int_a^bf(\varphi(t))\varphi'(t)dt \]
\( D \) 内の曲線の表示の仕方にはいろいろあります。
次の3つはすべて同じ単位円周を表す。
$$ \varphi(t)=\cos t+i\sin t \quad (0≦t≦2\pi) $$
$$ \psi(t)=\cos \frac{t}{2\pi}+i\sin \frac{t}{2\pi} \quad (0≦t≦4\pi^2) $$
$$ \phi(t)=\cos (2\pi t)+i\sin (2\pi t) \quad (0≦t≦1) $$
よって、複素積分が曲線の表示の仕方に依らないことを示す必要があります。
\( D \) 内の曲線 \( C \) の2つの表現 \( \varphi(t) \ (a≦t≦b) \) と \( \psi(s) \ (\alpha≦s≦\beta) \) に対して次が成り立つ。
\[ \int_a^bf(\varphi(t))\varphi'(t)dt=\int_{\alpha}^{\beta}f(\psi(s))\psi'(s)ds \]
定理1の証明(気になる方だけクリックしてください)
もう少しお待ちください。
\( \displaystyle \int_Czdz \) を下図の \( C_1,C_2 \) に沿って積分する。
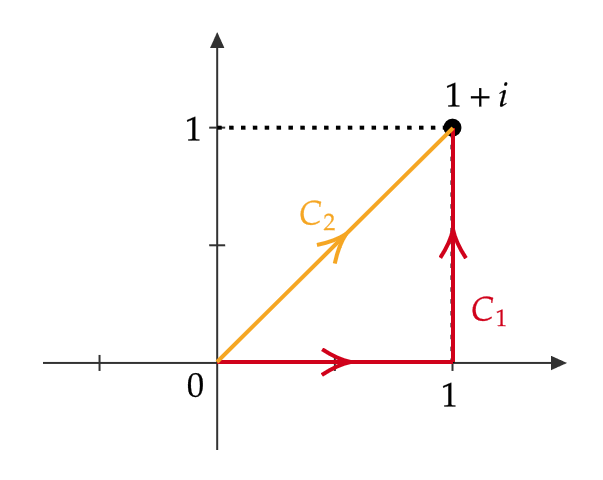
$$ C_1:\varphi(t)=\begin{cases} t & (0≦t≦1) \\ 1+i(t-1) & (1≦t≦2) \end{cases} $$
とかけるので、
$$ \begin{align} \int_{C_1}zdz&=\int_0^1\varphi(t)\varphi'(t)dt+\int_1^t\varphi(t)\varphi'(t)dt \\ &=\int_0^1t\cdot 1dt+\int_1^2(1+i(t-1))\cdot i dt=i \end{align} $$
一方で、
$$ C_2:\psi(t)=s+is \ (0≦s≦1) $$
とかけるので、
$$ \int_{C_2}zdz=\int_0^1(s+is)(1+i)ds=i $$
\( z_0\in \mathbb{C}, \ r>0 \) に対して、 \( C:z_0+re^{i\theta} \ (0≦\theta≦2\pi) \) とおく。
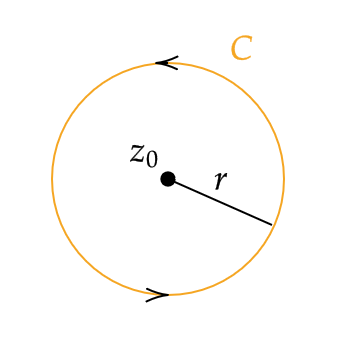
\( n\in\mathbb{N} \) に対して、 \( \displaystyle \int_C(z-z_0)^ndz \) を求める。
(1) \( n=-1 \) のとき \( (z_0+re^{i\theta})’=ire^{i\theta} \) より、
\[ \begin{align} \int_C(z-z_0)^{-1}dz&=\int_0^{2\pi}((z_0+re^{i\theta})-z_0)^{-1}\cdot ire^{i\theta}d\theta \\ &=\int_0^{2\pi}\frac{ire^{i\theta}}{re^{i\theta}}d\theta=i\int_0^{2\pi}d\theta=2\pi i \end{align} \]
(2) \( i\not=-1 \) のとき
\[ \begin{align} \int_C(z-z_0)^ndz&=\int_0^{2\pi}((z_0+re^{i\theta})-z_0)^n\cdot ire^{i\theta}d\theta \\ &=ir^{n+1}\int_0^{2\pi}e^{i(n+1)\theta}d\theta=ir^{n+1}\left[ \frac{1}{i(n+1)}e^{i(n+1)\theta}\right]^{2\pi}_0=0 \end{align} \]
例3をまとめると次のようになります。
\( z_0\in \mathbb{C}, \ r>0 \) に対して、 \( C:z_0+re^{i\theta} \ (0≦\theta≦2\pi) \) とおくと、 \( n\in\mathbb{Z} \) に対して次が成り立つ。
\[ \int_C(z-z_0)^ndz=\begin{cases} 0 & (n\not= -1) \\ 2\pi i & (n=-1) \end{cases} \]
最後に複素積分の簡単な性質を見ていきましょう。
\( f(z),g(z) \) を領域 \( D \) で定義された連続関数、 \( C \) を \( D \) 内の曲線とする。
(1) \( \alpha,\beta \) を複素定数とすると、
\[ \int_C(\alpha f(z)+\beta g(z))dz=\alpha \int_Cf(z)dz+\beta\int_Cg(z)dz \]
(2) 積分路 \( C:z=z(t) \ (a≦t≦b) \) を途中で2つの積分路
\[ C_1:z=z(t) \ (a≦t≦c), \quad C_2:z=z(t) \ (c≦t≦b) \]
に分けるとき、 \( C=C_1+C_2 \) とおけば、
\[ \int_{C_1+C_2}f(z)dz=\int_{C_1}f(z)dz+\int_{C_2}f(z)dz \]
(3) 曲線の向きを逆にした曲線を \( -C \) と表すと、
\[ \int_{-C}f(z)dz=-\int_Cf(z)dz \]
定理3の証明(気になる方だけクリックしてください)
もう少しお待ちください。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

