こんにちは、ひかりです。
今回は複素関数論から複素関数の初等関数の定義について解説していきます。
この記事では以下のことを紹介します。
- 複素関数の指数関数の定義について
- 複素関数の三角関数の定義について
- 複素関数の対数関数の定義について
複素関数の指数関数の定義
指数関数 \( y=e^x \) は \( x\in\mathbb{R} \) の場合はマクローリン展開より次のように表されます。
\[ e^x=\sum_{n=0}^{\infty}\frac{1}{n!}x^n=1+x+\frac{1}{2!}x^2+\cdots+\frac{1}{n!}x^n+\cdots \]
これを複素関数に拡張することを考えます。つまり、 \( z\in \mathbb{C} \) に対して次のベキ級数を考えます。
\[ \sum_{n=0}^{\infty}\frac{1}{n!}z^n=1+z+\frac{1}{2!}z^2+\cdots+\frac{1}{n!}z^n+\cdots \]
この級数は複素関数論05の例1(2)より収束半径は \( \infty \) となり、複素平面全体で収束します。
また、複素関数論05の定理3よりこの級数は正則関数となります。
よって、複素関数の指数関数を次で定義します。
\( z\in\mathbb{C} \) に対して指数関数 \( w=e^z \) を次で定義する。
\[ e^z=\sum_{n=0}^{\infty}\frac{1}{n!}z^n=1+z+\frac{1}{2!}z^2+\cdots+\frac{1}{n!}z^n+\cdots \]
実数の場合と同様に、指数関数の性質として次が成り立ちます。
\( z_1,z_2 \in\mathbb{C} \) に対して次が成り立つ。
\[ e^{z_1+z_2}=e^{z_1}e^{z_2} \]
\[ (e^z)’=e^z \]
また、複素関数の指数関数と実関数の三角関数との間の関係として、次のことが成り立ちます。
(1) \( \theta\in\mathbb{R} \) に対して次が成り立つ。
\[ e^{i\theta}=\cos \theta+i\sin \theta \]
(2) 複素数 \( z=x+iy \) に対して次が成り立つ。
\[ e^z=e^x(\cos y+i\sin y) \]
定理3の証明(気になる方だけクリックしてください)
(1) 定義1において、 \( z=i\theta \) とおくと、
$$ \begin{align} e^{i\theta}&=1+\frac{i\theta}{1!}+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!}+\cdots+\frac{(i\theta)^n}{n!}+\cdots \\ &=\left( 1-\frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4-\cdots+(-1)^m\frac{1}{(2m)!}\theta^{2m}+\cdots \right) \\ & \quad \quad +i\left( \theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5-\cdots+(-1)^m\frac{1}{(2m+1)!}\theta^{2m+1}+\cdots \right) \\ &=\cos\theta+i\sin\theta \end{align} $$
(2) 定理1より、
\[ e^z=e^{x+iy}=e^xe^{iy} \]
よって、(1)より、
\[ e^z=e^xe^{iy}=e^x(\cos y+i\sin y) \]
複素関数の三角関数の定義
指数関数と同様に複素関数の三角関数を実関数の三角関数のマクローリン展開を用いて次のように定義します。
\( z\in\mathbb{C} \) に対して三角関数 \( w=\sin z, \ w=\cos z, \ w=\tan z \) を次で定義する。
$$ \begin{align*} \sin z&=\sum_{m=0}^{\infty}(-1)^m\frac{1}{(2m+1)!}z^{2m+1} \\ &=z-\frac{1}{3!}z^3+\frac{1}{5!}z^5-\cdots+(-1)^m\frac{1}{(2m+1)!}z^{2m+1}+\cdots, \\ \cos z&=\sum_{m=0}^{\infty}(-1)^m\frac{1}{(2m)!}z^{2m} \\ &=1-\frac{1}{2!}z^2+\frac{1}{4!}z^4-\cdots+(-1)^m\frac{1}{(2m)!}z^{2m}+\cdots, \\ \tan z&=\frac{\sin z}{\cos z} \end{align*} $$
複素関数の指数関数と複素関数の三角関数との間の関係として、次のことが成り立ちます。
任意の \( z\in \mathbb{C} \) に対して次が成り立つ。
(1) \[ e^{iz}=\cos z+i\sin z \]
(2) \[ \sin z=\frac{e^{iz}-e^{-iz}}{2i}, \quad \cos z=\frac{e^{iz}+e^{-iz}}{2} \]
(3) \[ e^z=e^{z+2\pi i} \]
また、実関数と同様に次の性質が成り立ちます。
\( z,w\in\mathbb{C} \) に対して、
$$ \begin{align} \sin (z+w)&=\sin z\cos w+\cos z\sin w \\ \cos (z+w)&=\cos z\cos w-\sin z\sin w \end{align} $$
\[ (\cos z)’=-\sin z, \quad (\sin z)’=\cos z \]
定理4(2)より、 \( z \) が虚軸上にあるとき、
\[ \cos z=\cos (iy)=\frac{e^{y}+e^{-y}}{2}\to \infty \ (y\to\infty) \]
となるので、複素数 \( z \) に対しては \( |\cos z|≦1 \) は成り立ちません。
同様に、複素数 \( z \) に対して \( |\sin z|≦1 \) も成り立ちません。
\( \cos z=2 \) となる \( z\in\mathbb{C} \) を求める。
\( \cos z=\frac{e^{iz}+e^{-iz}}{2}=2 \) より、 \( e^{iz}+e^{-iz}=4 \)
\( \zeta=e^{iz} \) とおくと、 \( \zeta+\frac{1}{\zeta}=4 \) すなわち、
\[ \zeta^2-4\zeta+1=0 \]
であるので、 \( \zeta=2\pm \sqrt{3} \) ここで、 \( z=x+iy \) とおくと、
\[ e^{iz}=e^{-y+ix}=e^{-y}(\cos x+i\sin x)=2\pm \sqrt{3} \]
より、
\[ \sin x=0, \quad e^{-y}\cos x=2\pm \sqrt{3}>0 \ (つまり \cos x>0) \]
となり、 \( x=2n\pi \ (n\in\mathbb{N}) \) より \( \cos x=1 \)
したがって、 \( e^{-y}=2\pm \sqrt{3} \) より、 \( -y=\log (2\pm \sqrt{3}) \) であるので、
\[ z=2n\pi -i\log (2\pm \sqrt{3}) \ (n\in\mathbb{N}) \]
複素関数の対数関数の定義
\( x\in \mathbb{R}, \ y>0 \) に対して、
\[ y=\log x \ \iff \ x=e^y \]
という関係がありました。
よって、複素関数においても \( e^z \) の逆関数として \( \log z \) を定義をすることを考えます。
しかし、定理4(3)より \( e^z=e^{z+2\pi i} \) となるので、 \( w\in\mathbb{C} \) に対して \( w=e^z \) となる \( z\in \mathbb{C} \) はただ一つに定まりません。
実際、 \( w=re^{i\theta} \) と表すと、 \( n\in \mathbb{N} \) に対して
\[ e^{\log r+i(\theta+2\pi n)}=e^{\log r}e^{i(\theta+2\pi n)}=re^{i\theta}=w \]
であるので、 \( w=e^z \) の \( z\in \mathbb{C} \) についての解は
\[ z=\log r+i(\theta+2\pi n)=\log |w|+i(\text{arg} \ w+2\pi n) \]
(ここで、 \( \text{arg} \ w \) は \( w \) の偏角)
つまり、
\[ \log w=\log |w|+i(\text{arg} \ w+2\pi n) \]
となり多価関数となってしまいます。
そこで、 \( z\in \mathbb{C} \) の偏角 \( \text{arg} \ z \) に対して \( \text{arg} \ z+2\pi \) もまた \( z \) の偏角となるので \( -\pi<\text{arg} \ z≦\pi \) に制限して考えます。
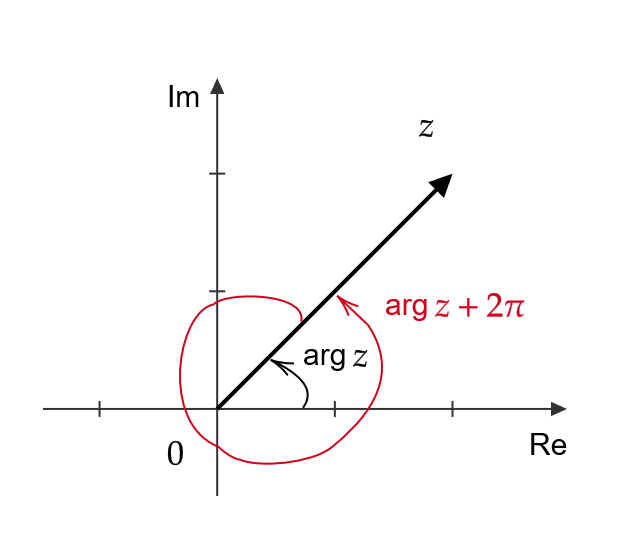
これにより、対数関数を次のように定めます。
\( z=re^{i\theta}\in\mathbb{C} \) に対して対数関数 \( w=\log z \) を次で定義する。
\[ \log z=\log |z|+i\text{arg} \ z (=\log |z|+i(\text{arg} \ z+2\pi n)) \]
また、 \( z\in \mathbb{C} \) に対して偏角の主値 \( \text{Arg} \ z \) を次で定義する。
\[ \text{Arg} \ z=\text{arg} z \quad (-\pi<\text{arg} \ z≦\pi) \]
そして、対数関数の主値 \( \text{Log} \ z \) を次で定義する。
\[ \text{Log} \ z=\log |z|+i\text{Arg} \ z \]
(1) $$ \begin{align*} \log (-5)&=\log |-5|+i(\text{arg} \ (-5)+2\pi n) \\ &=\log 5+(2n+1)\pi n \end{align*} $$
(2) $$ \text{Log} \ (-1)=\log|-1|+i\text{Arg} \ (-1)=\log 1+i\pi=i\pi $$
(3) $$ \begin{align*} \text{Log} \ (1+i)&=\log |1+i|+i\text{Arg} \ (1+i) \\ &=\log \sqrt{2}+i\frac{\pi}{4}=\frac{1}{2}\log 2+i\frac{\pi}{4} \end{align*} $$
最後に、対数関数の性質を紹介します。
\( \text{Log} \ z \) は \( \mathbb{C}\backslash (-\infty,0] \) 上で正則であり、
\[ \frac{d}{dz}\text{Log} \ z=\frac{1}{z} \quad (z\in\mathbb{C}\backslash (-\infty,0]) \]
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

