こんにちは、ひかりです。
今回は曲線・曲面論から平面曲線のフレネ・セレーの公式と曲率の表示について解説していきます。
この記事では以下のことを紹介します。
- 平面曲線のフレネ・セレーの公式について
- 曲率の具体的な表示について
平面曲線のフレネ・セレーの公式
曲線・曲面論02の記事にて、弧長パラメータを用いた平面曲線の曲率の定義を紹介しました。
ここでは、その曲率 \( \kappa(s) \) を用いた接ベクトル \( \mathbf{p}’ \) と単位法線ベクトル \( \mathbf{n} \) の導関数の表現について見ていきましょう。
\( \mathbf{n} \) は単位法線ベクトルより \( \|\mathbf{n}(s)\|^2\equiv 1 \) であるので、これを \( s \) で微分すると、 \( \mathbf{p}'(s) \) と \( \mathbf{n}(s) \) が直交することから
$$ \mathbf{n}(s)\cdot \mathbf{n}'(s)=0 \ \Rightarrow \ \mathbf{n}'(s) \ と \ \mathbf{p}'(s) \ は平行 $$
よって、 \( \mathbf{n}'(s)=\lambda(s)\mathbf{p}'(s) \) と表せます。このとき、 \( \|\mathbf{p}'(s)\|\equiv 1 \) と曲線・曲面論02の式(2)より、
$$ \lambda(s)=\lambda(s)\mathbf{p}'(s)\cdot \mathbf{p}'(s)=\mathbf{n}'(s)\cdot \mathbf{p}'(s)=-\kappa(s) $$
曲線・曲面論02の式(1)と合わせると、次のことが成り立ちます。
平面曲線の位置ベクトルを \( \mathbf{p}(s) \) とする。ただし、 \( s \) は弧長パラメータとする。
このとき、次が成り立つ。
$$ \mathbf{p}^{\prime\prime}(s)=\kappa(s)\mathbf{n}(s), \quad \mathbf{n}'(s)=-\kappa(s)\mathbf{p}'(s) $$
これは次のように表せる。
$$ \frac{d}{ds}\begin{pmatrix} \mathbf{p}’ \\ \mathbf{n} \end{pmatrix}=\begin{pmatrix} 0 & \kappa \\ -\kappa & 0 \end{pmatrix}\begin{pmatrix} \mathbf{p}’ \\ \mathbf{n} \end{pmatrix} $$
この定理を用いると、位置ベクトルのテイラー展開による表示を与えることができます。
そのための準備として次を定義します。
ランダウのスモール・オーダー \( o \) とラージ・オーダー \( O \) を次で定める。
$$ v(t)=o(u(t)) \ (t\to t_0) \ \overset{\text{def}}{\Longleftrightarrow} \ \lim_{t\to t_0}\frac{v(t)}{u(t)}=0 $$
$$ v(t)=O(u(t)) \ (t\to t_0) \ \overset{\text{def}}{\Longleftrightarrow} \ \lim_{t\to t_0}\left|\frac{v(t)}{u(t)}\right|<\infty $$
ベクトル値関数 \( \mathbf{v}(t) \) の場合は、
$$ \mathbf{v}(t)=o(u(t)) \ (t\to t_0) \ \overset{\text{def}}{\Longleftrightarrow} \ \lim_{t\to t_0}\frac{\|\mathbf{v}(t)\|}{u(t)}=0 $$
$$ \mathbf{v}(t)=O(u(t)) \ (t\to t_0) \ \overset{\text{def}}{\Longleftrightarrow} \ \lim_{t\to t_0}\frac{\|\mathbf{v}(t)\|}{|u(t)|}<\infty $$
これを用いると、次が成り立ちます。
定理1の状況で \( \mathbf{p} \) は \( C^2 \)-級とする。
このとき、 \( \mathbf{p}(s) \) の \( s=s_0 \) を中心とするテイラー展開は次のようになる。
$$ \mathbf{p}(s)=\mathbf{p}(s_0)+\mathbf{p}'(s_0)(s-s_0)+\frac{1}{2}\kappa(s_0)\mathbf{n}(s_0)(s-s_0)^2+o((s-s_0)^2) \ (s\to s_0) $$
定理2の証明(気になる方だけクリックしてください)
テイラーの定理より、
$$ \mathbf{p}(s)=\mathbf{p}(s_0)+\mathbf{p}'(s_0)(s-s_0)+\frac{1}{2}\mathbf{p}^{\prime\prime}(s_0)(s-s_0)^2+o((s-s_0)^2) \quad (s\to s_0) $$
これにフレネ・セレーの公式の \( \mathbf{p}^{\prime\prime}(s_0)=\kappa(s_0)\mathbf{n}(s_0) \) を代入すれば成り立ちます。
曲率の具体的な表示
ここでは、さまざまな曲率 \( \kappa \) の具体的な表示について見ていきましょう。
\( \mathbf{p}(s)=(x(s),f(x(s))) \) とする。ただし、 \( s \) は弧長パラメータとする。
また、 \( \varphi(x)=\frac{1}{\sqrt{1+\left( \frac{df}{dx}(x)\right)^2}} \) とおく。
このとき、次が成り立つ。
$$ \kappa=\frac{d}{dx}\left(\varphi(x)\frac{df}{dx}(x)\right)=\frac{d}{dx}\left( \frac{d}{ds}f(x(s))\right) =\frac{1}{\varphi(x)}\frac{d^2}{ds^2}f(x(s)) $$
定理3の証明(気になる方だけクリックしてください)
(初めの等号) $$ \kappa=(\varphi(x))^3\frac{d^2f}{dx^2}(x) $$
$$ \frac{d}{dx}\left(\varphi(x)\frac{df}{dx}(x)\right)=\frac{d\varphi}{dx}(x)\frac{df}{dx}(x)+\varphi(x)\frac{d^2f}{dx^2}(x) $$
であるので、
$$ \frac{d\varphi}{dx}(x)\frac{df}{dx}(x)+\varphi(x)\frac{d^2f}{dx^2}(x)=(\varphi(x))^3\frac{d^2f}{dx^2}(x) $$
を示せばよいです。ここでは、
$$ \frac{d\varphi}{dx}(x)\frac{df}{dx}(x)=\varphi(x)\frac{d^2f}{dx^2}(x)((\varphi(x))^2-1) $$
を示します。
$$ \begin{align} \frac{d\varphi}{dx}(x)&=\frac{d}{dx}\left(\left( 1+\left( \frac{df}{dx}(x)\right)^2\right)^{-\frac{1}{2}}\right)’ \\ &=-\frac{1}{2}\left( 1+\left( \frac{df}{dx}(x) \right)^2 \right)^{-\frac{3}{2}}\cdot \frac{d}{dx}\left( 1+\left( \frac{df}{dx}(x)\right)^2 \right) \\ &=-\left( 1+\left( \frac{df}{dx}(x)\right)^2 \right)^{-\frac{3}{2}}\cdot \frac{df}{dx}(x)\frac{d^2f}{dx^2}(x) \\ &=-(\varphi(x))^3\frac{df}{dx}(x)\frac{d^2f}{dx^2}(x) \end{align} $$
$$ \begin{align} ((\varphi(x))^2-1)&=\left( \frac{1}{1+\left( \frac{df}{dx}(x)\right)^2}-1 \right) \\ &=-\left( 1+\left( \frac{df}{dx}(x)\right)^2\right)^{-1}\left( \frac{df}{dx}(x)\right)^2 \\ &=-(\varphi(x))^2\left( \frac{df}{dx}(x)\right)^2 \end{align} $$
となるので、
$$ \frac{d\varphi}{dx}(x)\frac{df}{dx}(x)=-(\varphi(x))^3\left( \frac{df}{dx}(x)\right)^2\frac{d^2f}{dx^2}(x)=\varphi(x)\frac{d^2f}{dx^2}(x)((\varphi(x))^2-1) $$
が成り立ち、1つ目の等号が示せました。
(2つ目の等号)
$$ \frac{d}{dx}\left( \frac{d}{ds}f(x(s)) \right)=\frac{d}{dx}\left( \frac{dx}{ds}\frac{d}{dx}f(x(s)) \right)=\frac{d}{dx}\left( \varphi(x)\frac{df}{dx}(x) \right) $$
(3つ目の等号)
$$ \begin{align} \frac{1}{\varphi(x)}\frac{d^2}{ds^2}f(x(s))&=\frac{1}{\varphi(x)}\frac{dx}{ds}\frac{d}{dx}\frac{d}{ds}f(x(s))=\frac{1}{\varphi(x)}\varphi(x)\frac{d}{dx}\left(\frac{d}{ds}f(x(s))\right) \\ &=\frac{d}{dx}\left(\frac{d}{ds}f(x(s))\right) \end{align} $$
\( \mathbf{p}'(s) \) と \( x \) 軸方向とのなす角を反時計回りに測ったものを \( \theta(s) \) とおきます。
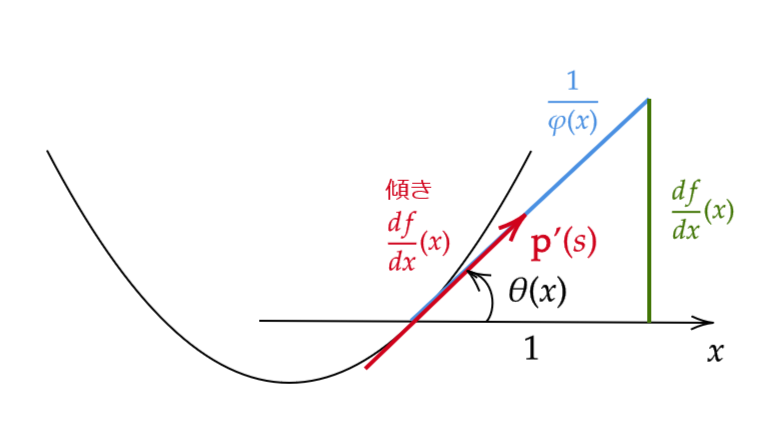
すると、 \( \tan\theta=\frac{df}{dx}(x(s)) \) であるので、
$$ \theta(s)=\arctan \frac{df}{dx}(x(s)) $$
また、このとき
$$ \mathbf{p}'(s)=(\cos \theta(s),\sin \theta(s)), \quad \mathbf{n}(s)=(-\sin \theta(s),\cos \theta(s)) $$
であるので、次が成り立ちます。
$$ \kappa(s)=\frac{d\theta}{ds}=\frac{d}{dx}\sin \theta(s) $$
定理4の証明(気になる方だけクリックしてください)
まず、初めの等号については
$$ \begin{align} \kappa(s)&=\mathbf{p}^{\prime\prime}(s)\cdot \mathbf{n}(s) \\ &=(-\theta'(s)\sin \theta(s),\theta'(s)\cos \theta(s))\cdot (-\sin \theta(s),\cos\theta(s))=\theta'(s) \end{align} $$
2つ目の等号については上の図の青い線から
$$ \sin \theta(s)=\varphi(x)\frac{df}{dx}(x) $$
であるので、定理3より
$$ \kappa(s)=\frac{d}{dx}\left( \varphi(x)\frac{df}{dx}(x)\right)=\frac{d}{dx}\sin \theta (s) $$
曲線 \( y=f(x) \) が \( x=x(t),y=y(t) \) という表示の場合
\( \dot{}=\frac{d}{dt} \) とすると、
$$ \frac{df}{dx}=\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{\dot{y}}{\dot{x}} $$
$$ \frac{d^2f}{dx^2}=\frac{d}{dx}\left( \frac{df}{dx} \right)=\frac{dt}{dx}\frac{d}{dt}\left( \frac{df}{dx} \right)=\frac{1}{\dot{x}}\frac{d}{dt}\left( \frac{\dot{y}}{\dot{x}}\right)=\frac{\dot{x}\ddot{y}-\ddot{x}\dot{y}}{\dot{x}^3} $$
したがって、曲率 \( \kappa \) は曲線・曲面論02の式(3)に上を代入することにより、
$$ \kappa(t)=\frac{f^{\prime\prime}(x)}{(1+(f'(x))^2)^{\frac{3}{2}}}=(\text{sgn} \ \dot{x}(t))\frac{\dot{x}(t)\ddot{y}(t)-\ddot{x}(t)\dot{y}(t)}{\{(\dot{x}(t))^2+(\dot{y}(t))^2\}^{\frac{3}{2}}} $$
ここで、 \( \text{sgn} \ \dot{x}(t) \) は \( \dot{x}(t) \) の符号となります。
曲線が \( F(x,y)=0 \) で与えられている場合
陰関数定理より \( F_y\not=0 \) であれば、 \( F(x,y)=0 \) は局所的に \( y=f(x) \) と \( y \) について解くことができるので、
$$ \frac{df}{dx}=-\frac{F_x}{F_y}, \quad \frac{d^2f}{dx^2}=-\frac{F_{xx}F_y^2-2F_{xy}F_xF_y+F_{yy}F_x^2}{F_y^2} $$
これらを \( \kappa \) の式に代入すると、
$$ \begin{align} \kappa&=\frac{f^{\prime\prime}(x)}{(1+(f'(x))^2)^{\frac{3}{2}}}=-(\text{sgn} \ F_y)\frac{F_{xx}F_y^2-2F_{xy}F_xF_y+F_{yy}F_x^2}{(F_x^2+F_y^2)^{\frac{3}{2}}} \\ &=\frac{-(\text{sgn} \ F_y)}{(F_x^2+F_y^2)^{\frac{3}{2}}}(-F_y,F_x)\text{Hess} \ F \begin{pmatrix} -F_y \\ F_x \end{pmatrix} \end{align} $$
ここで、 \( \text{Hess} \ F=\begin{pmatrix} F_{xx} & F_{xy} \\ F_{yx} & F_{yy} \end{pmatrix} \) は \( F \) のヘッセ行列であり、 \( -(\text{sgn} \ F_y) \) は向きの指定、 \( \begin{pmatrix} -F_y \\ F_x \end{pmatrix} \) は接ベクトル、 \( (F_x^2+F_y^2)^{-\frac{3}{2}} \) は大きさの正規化を表します。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

