こんにちは、ひかりです。
今回は曲線・曲面論から弧長パラメータによる平面曲線の曲率の定義について解説していきます。
この記事では以下のことを紹介します。
- 平面曲線の長さについて
- 弧長パラメータについて
- 弧長パラメータによる平面曲線の曲率の定義について
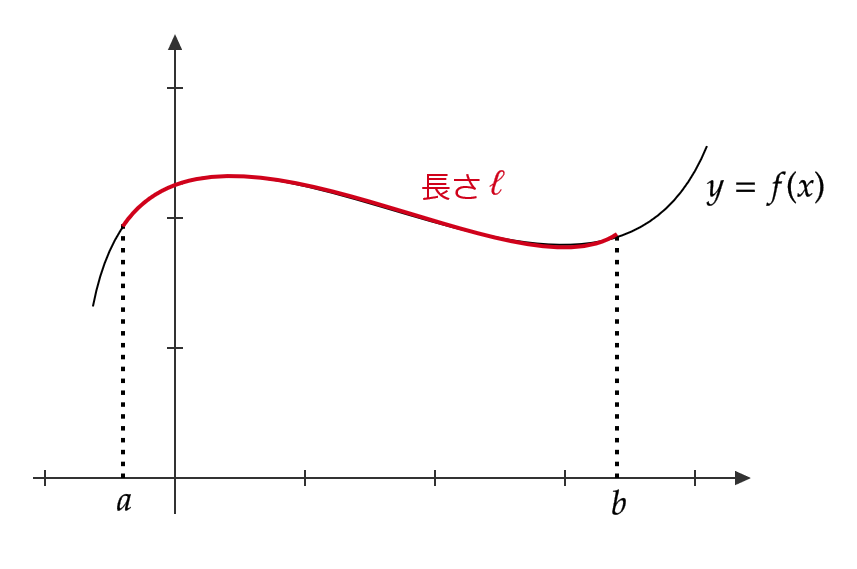
平面曲線の長さ
微分積分学15で紹介した平面曲線の長さについて再び考えてみましょう。
\( f \) を \( [a,b] \) 上微分可能、 \( \sqrt{1+(f’)^2} \) を \( [a,b] \) 上積分可能とする。
( \( f\in C^1[a,b] \) であれば十分である)
このとき、 \( xy \) 平面内の曲線 \( y=f(x) \ (a≦x≦b) \) の長さ \( \ell \) は
\[ \ell=\int_a^b\sqrt{1+(f'(x))^2}dx \]
定理1の証明(気になる方だけクリックしてください)
$$ \Delta:a=x_0<x_1<x_2<\cdots<x_n=b $$
を \( [a,b] \) の分割として、点 \( (x_j,f(x_j)) \) を結ぶ折れ線で曲線 \( f \) を近似します。すると、
$$ \begin{align} 折れ線の長さ&=\sum_{j=1}^n\sqrt{(x_j-x_{j-1})^2+(f(x_j)-f(x_{j-1}))^2} \\ &=\sum_{j=1}^n\sqrt{1+\left( \frac{f(x_j)-f(x_{j-1})}{x_j-x_{j-1}} \right)^2} \delta_j \quad (\delta_j=x_j-x_{j-1}) \end{align} $$
平均値の定理より、ある \( \xi_j\in (x_{j-1},x_j) \) が存在して、
$$ \frac{f(x_j)-f(x_{j-1})}{x_j-x_{j-1}}=f'(\xi_j) $$
したがって、
$$ 折れ線の長さ=R\left[\{\xi_j\},\Delta,\sqrt{1+(f’)^2}\right]\to \int_a^b\sqrt{1+(f'(x))^2}dx \ (n\to \infty) $$
ここで、 \( R[\{\xi_j\},\Delta,f] \) は \( \{\xi_j\} \) を選んだときの \( f \) のリーマン和です。
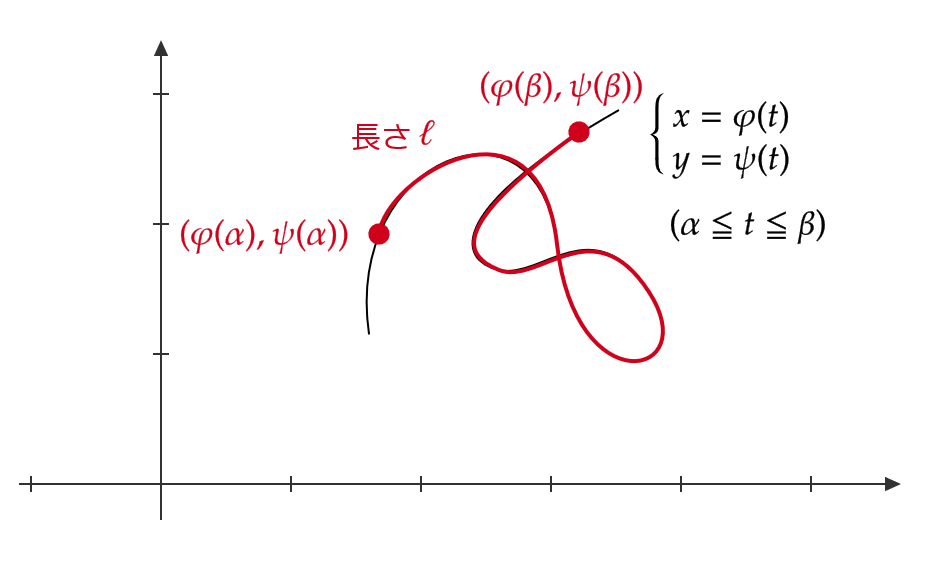
さらに媒介変数表示された曲線の長さは次のようになります。
\( \varphi,\psi \) を \( [\alpha,\beta] \) 上微分可能、 \( \sqrt{(\dot{\varphi})^2+(\dot{\psi})^2} \) を \( [\alpha,\beta] \) 上積分可能とする。
(ここで、 \( \dot{}=\frac{d}{dt} \) である。 \( \varphi,\psi\in C^1[\alpha,\beta] \) であれば十分である)
このとき、
\[ x=\varphi(t), \ y=\psi(t), \quad (\alpha≦t≦\beta) \]
で表される \( xy \) 平面内の曲線の長さ \( \ell \) は
\[ \ell=\int_{\alpha}^{\beta}\sqrt{(\dot{\varphi}(t))^2+(\dot{\psi}(t))^2}dt \]
定理2の証明(気になる方だけクリックしてください)
必要であれば、 \( t \) の範囲を狭くして座標を回転させることにより、曲線が \( y=f(x) \ (a≦x≦b) \) の形で表されているとします。
$$ \psi(t)=f(\varphi(t)), \ \psi(\alpha)=a, \ \psi(\beta)=b, \ \dot{\psi}(t)=\frac{df}{dx}(\varphi(t))\cdot \dot{\varphi}(t) $$
とすると、定理1より
$$ \begin{align} \ell&=\int_a^b\sqrt{1+\left( \frac{df}{dx}(x)\right)^2}dx=\int_{\alpha}^{\beta}\sqrt{1+\left( \frac{df}{dx}(\varphi(t))\right)^2}\dot{\varphi}(t)dt \\ &=\int_{\alpha}^{\beta}\sqrt{(\dot{\varphi}(t))^2+\left( \frac{df}{dx}(\varphi(t))\cdot \dot{\varphi}(t)\right)^2}dt=\int_{\alpha}^{\beta}\sqrt{(\dot{\varphi}(t))^2+(\dot{\psi}(t))^2}dt \end{align} $$
弧長パラメータ
曲線が \( y=f(x) \) で表されているとして、
$$ s=s(x)=\int_a^x\sqrt{1+(f'(x))^2}dx $$
とします。
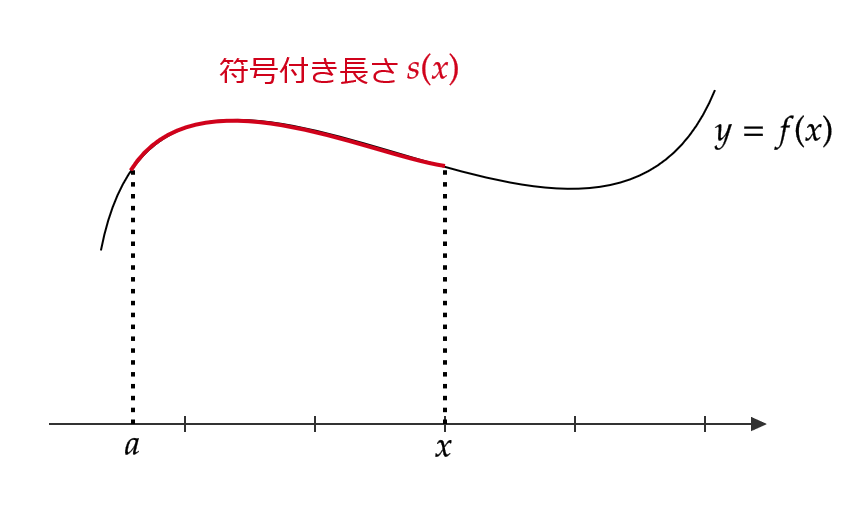
このとき、逆関数を \( x=x(s), \ y(s)=f(x(s)) \) とおくことにより、曲線は \( s \) をパラメータとして、
$$ \begin{cases} x=x(s) \\ y=y(s)(=f(x(s))) \end{cases} $$
と表されます。
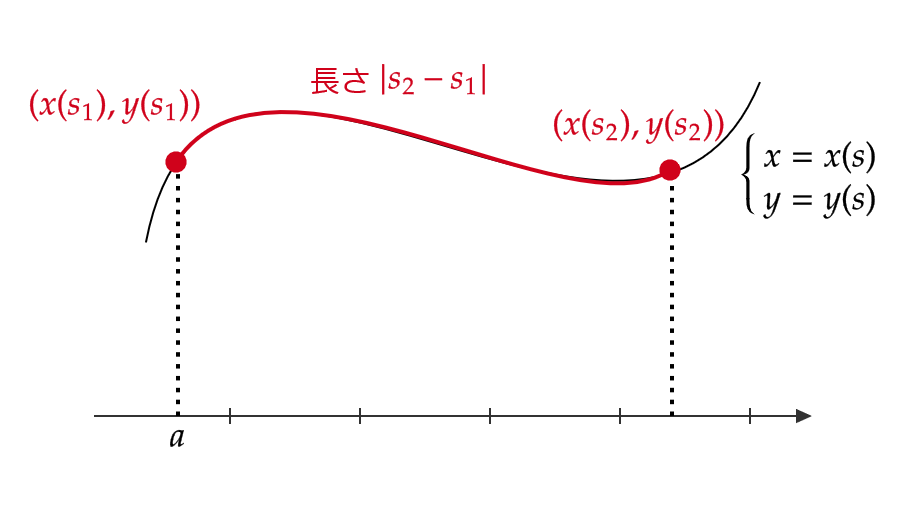
このパラメータ \( s \) のことを弧長パラメータといいます。ここで、
$$ \mathbf{p}(s)=(x(s),y(s))=(x(s),f(x(s))) $$
とおきます。すると、曲線はベクトル値関数 \( \mathbf{p}(s) \) の終点の軌跡となります。
(つまり、 \( \mathbf{p}(s) \) は曲線の位置ベクトルとなります。)
ここで、 \( {}’=\frac{d}{ds} \) と書くことにすると、 \( \mathbf{p}'(s)=(x'(s),y'(s)) \) は接ベクトルとなります。
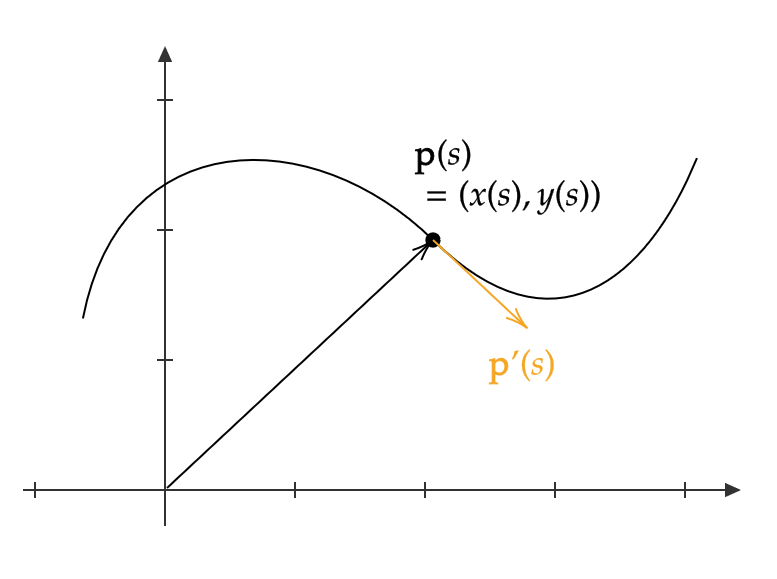
また、
$$ x'(s)=\frac{dx}{ds}=\frac{1}{\frac{ds}{dx}}=\frac{1}{\sqrt{1+(f'(x))^2}} $$
より、
$$ \mathbf{p}'(s)=\frac{d}{ds}(x(s),f(x(s)))=\frac{dx}{ds}\frac{d}{dx}(x,f(x))|_{x=x(s)}=\frac{1}{\sqrt{1+(f'(x))^2}}(1,f'(x(s))) $$
であるので、弧長パラメータについて次のことが成り立ちます。
$$ \|\mathbf{p}'(s)\|=1 \quad (任意のs) $$
弧長パラメータによる平面曲線の曲率の定義
弧長パラメータを用いて平面曲線の曲率を定義してみましょう。
まず、 \( \mathbf{p}'(s) \) を反時計回りに \( \frac{\pi}{2} \) だけ回転して得られるベクトル
$$ \mathbf{n}(s)=\frac{1}{\sqrt{1+(f'(x(s)))^2}}(-f'(x(s)),1) $$
は単位法線ベクトルとなります。
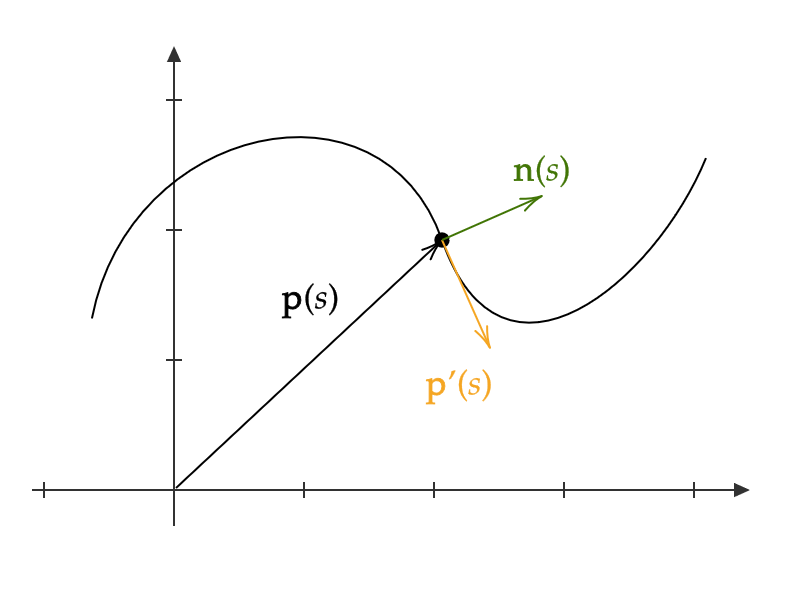
\( \|\mathbf{p}'(s)\|\equiv 1 \) であるので、
$$ \begin{align} 0&=\frac{d}{ds}\|\mathbf{p}'(s)\|^2=\frac{d}{ds}(\mathbf{p}'(s),\mathbf{p}'(s)) \\ &=\mathbf{p}^{\prime\prime}(s)\cdot \mathbf{p}'(s)+\mathbf{p}'(s)\cdot \mathbf{p}^{\prime\prime}(s)=2\mathbf{p}'(s)\cdot \mathbf{p}^{\prime\prime}(s) \end{align} $$
と書けます。したがって、 \( \mathbf{p}^{\prime\prime} \) は \( \mathbf{p}’ \) と直交します。
つまり、 \( \mathbf{p}^{\prime\prime} \) は \( \mathbf{n} \) と平行となるので、ある \( \kappa(s) \) が存在して、
$$ \mathbf{p}^{\prime\prime}(s)=\kappa(s)\mathbf{n}(s), \quad \kappa(s)=\kappa(s)\mathbf{n}(s)\cdot\mathbf{n}(s)=\mathbf{n}(s)\cdot \mathbf{p}^{\prime\prime}(s) \tag{1} $$
と表せます。この \( \kappa \) を \( f \) とその導関数を用いて表してみましょう。
\( \mathbf{n}(s)\cdot \mathbf{p}'(s)\equiv 0 \) より、両辺を \( s \) で微分すると、
$$ 0=(\mathbf{n}(s)\cdot \mathbf{p}'(s))’=\mathbf{n}'(s)\cdot \mathbf{p}'(s)+\mathbf{n}(s)\cdot \mathbf{p}^{\prime\prime}(s)=\mathbf{n}'(s)\cdot \mathbf{p}'(s)+\kappa (s) $$
であるので、
$$ \kappa(s)=-\mathbf{n}'(s)\cdot \mathbf{p}'(s)=-\frac{dx}{ds}\frac{d}{dx}\mathbf{n}(s(x))\cdot \mathbf{p}'(s(x)) \tag{2} $$
ここで、 \( \varphi(x)=\frac{1}{\sqrt{1+(f'(x))^2}}=\frac{dx}{ds} \) とおくと、
$$ \frac{d}{dx}\mathbf{n}(s(x))=\frac{d}{dx}\{\varphi(x)(-f'(x),1)\}=\varphi'(x)(-f'(x),1)+\varphi(x)(-f^{\prime\prime}(x),0) $$
$$ \mathbf{p}'(s(x))=\varphi(x)(1,f'(x)) $$
したがって、
$$ \begin{align} \kappa&=-\varphi(x)\{\varphi'(x)(-f'(x),1)+\varphi(x)(-f^{\prime\prime}(x),0)\}\cdot \varphi(x)(2,f'(x)) \\ &=\varphi^3f^{\prime\prime}(x)=\frac{f^{\prime\prime}(x)}{(1+(f'(x))^2)^{\frac{3}{2}}} \end{align} \tag{3} $$
と表せます。特に、 \( |\kappa|=k \) となります。(\(k\) は前回定義した曲率)
また、この \( \kappa(s) \) のことも平面曲線の曲率といいます。
半径 \( r \) の円の曲率 \( \kappa \) は次のようになる。
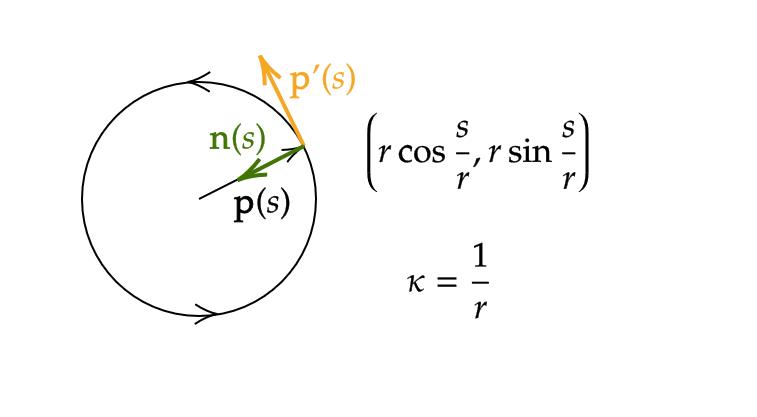
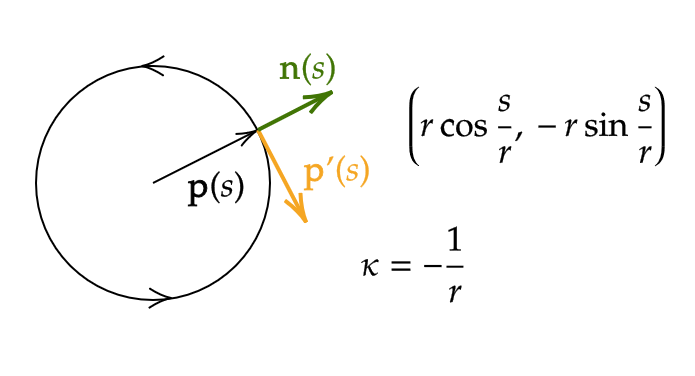
例1を見ると、 \( \kappa(s)\cdot \mathbf{n}(s) \) は曲線の向きに依存しません。よって、次を定めます。
$$ \boldsymbol{\kappa}(s)=\kappa(s)\cdot \mathbf{n}(s)=\mathbf{p}^{\prime\prime}(s) $$
を曲率ベクトルという。(見にくいですが、太文字の \( \kappa \) です)
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

