こんにちは、ひかりです。
今回は曲線・曲面論から円による平面曲線の曲率の定義について解説していきます。
この記事では以下のことを紹介します。
- 円を用いた平面曲線の曲率の定義について
- 平面曲線の曲率の具体的な表示について
円を用いた平面曲線の曲率の定義
まずは、平面曲線について考えていきます。
ある平面曲線に対して、その曲がり具合を表す量のことを曲率といいます。
では、どのようにして曲がり具合というのを数値化するのでしょうか。
そのために、円の曲率を次で定めます。
半径 \( r(>0) \) の円の曲率を \( \frac{1}{r} \) と定める。
ただし、直線は半径 \( \infty \) の円と考えて曲率 \( 0 \) とする。
これをもとに一般の平面曲線の曲率を定義してみましょう。
まず、一般に平面曲線は \( F(x,y)=0 \) のグラフで表されますが、座標をうまくとることにより陰関数定理から局所的に \( y=f(x) \) のグラフで表すことができます。
このとき、
$$ f(x) \ : \ 曲線の位置の情報をもつ量 $$
$$ \frac{df}{dx}(x) \ : \ 曲線の傾きの情報をもつ量 $$
$$ \frac{d^2f}{dx^2}(x) \ : \ 曲線の曲がり具合の情報をもつ量 $$
と言えます。したがって、次のように定めます。
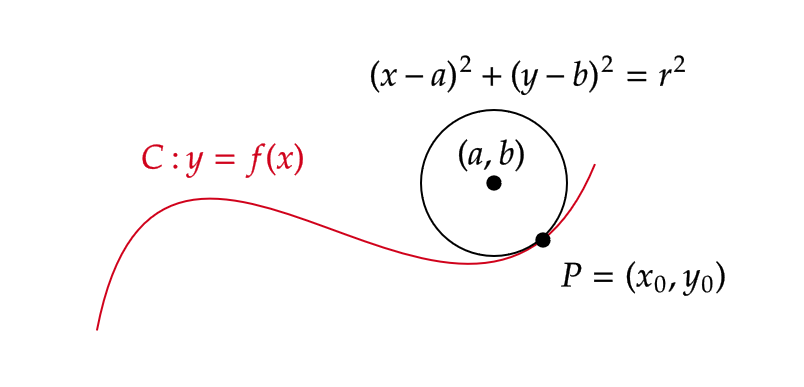
平面曲線 \( C \) 上の点 \( P \) において、 \( C \) に2次の接触をもつ円の曲率のことを \( C \) の点 \( P \) における曲率という。
ここで、曲線 \( y=f(x) \) が点 \( (x_0,f(x_0)) \) において曲線 \( y=g(x) \) に2次の接触をもつとは、次をみたすことをいう。
$$ f(x_0)=g(x_0), \quad \frac{df}{dx}(x_0)=\frac{dg}{dx}(x_0), \quad \frac{d^2f}{dx^2}(x_0)=\frac{d^2g}{dx^2}(x_0) $$
平面曲線の曲率の具体的な表示
この定義から、平面曲線 \( y=f(x) \) の曲率の具体的な表示を求めてみましょう。
定義2をみたす円を
$$ (x-a)^2+(y-b)^2=r^2 $$
とします。そして、点 \( P \) 上の近傍で \( y \) を \( x \) の関数 \( y=y(x) \) と見ます。つまり、
$$ (x-a)^2+(y(x)-b)^2=r^2 \tag{1} $$
これを2回 \( x \) で微分すると、
$$ 2(x-a)+2(y(x)-b)\frac{dy}{dx}(x)=0 \tag{2} $$
$$ 2+2\left( \frac{dy}{dx}(x)\right)^2+2(y(x)-b)\frac{d^2y}{dx^2}(x)=0 \tag{3} $$
ここで、 \( y=f(x) \) と \( y=y(x) \) は点 \( (x_0,f(x_0)) \) で2次の接触をもつので、
$$ f(x_0)=y(x_0), \quad \frac{df}{dx}(x_0)=\frac{dy}{dx}(x_0), \quad \frac{d^2f}{dx^2}(x_0)=\frac{d^2y}{dx^2}(x_0) $$
よって、これを式(1)-(3)に代入すると、
$$ (x_0-a)^2+(f(x_0)-b)^2=r^2 \tag{4} $$
$$ (x_0-a)+(f(x_0)-b)\frac{df}{dx}(x_0)=0 \tag{5} $$
$$ 1+\left( \frac{df}{dx}(x_0)\right)^2+(f(x_0)-b)\frac{d^2f}{dx^2}(x_0)=0 \tag{6} $$
式(4),(5)を組み合わせることにより、
$$ \begin{align} r^2&=(x_0-a)^2+(f(x_0)-b)^2=(f(x_0)-b)^2\left(\frac{df}{dx}(x_0)\right)^2+(f(x_0)-b)^2 \\ &=(f(x_0)-b)^2\left\{ \left( \frac{df}{dx}(x_0)\right)^2+1 \right\}=(*) \end{align} $$
ここで、 \( \frac{d^2f}{dx^2}(x_0)\not=0 \) とすると、式(6)より
$$ (*)=\frac{\left\{ 1+\left( \frac{df}{dx}(x_0)\right)^2 \right\}^2}{\left( \frac{d^2f}{dx^2}(x_0)\right)^2}\left\{ \left( \frac{df}{dx}(x_0) \right)^2+1 \right\} $$
したがって、
$$ \frac{1}{r}=\frac{\left|\frac{d^2f}{dx^2}(x_0)\right|}{\left\{ 1+\left( \frac{df}{dx}(x_0)\right)^2 \right\}^\frac{3}{2}} $$
よって、平面曲線の曲率を次で定義することもできます。
\( y=f(x) \) のグラフで表される平面曲線 \( C \) の点 \( (x_0,f(x_0)) \) における曲率 \( k \) を次で定める。
$$ k=\frac{\left|\frac{d^2f}{dx^2}(x_0)\right|}{\left\{ 1+\left( \frac{df}{dx}(x_0)\right)^2 \right\}^\frac{3}{2}} $$
(ここで、\( \frac{d^2f}{dx^2}(x_0)=0 \) のときもこの式から \( k=0 \) と定める。)
曲率の導出に現れた円を \( C \) の点 \( (x,f(x)) \) の曲率円といい、中心 \( (a,b) \) を曲率中心、 \( r \) を曲率半径といいます。
また、曲率中心の軌跡を \( C \) の縮閉線といい、 \( C \) を縮閉線とする曲線を伸開線といいます。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

