こんにちは、ひかりです。
今回は線形代数学から行列と一次変換について解説していきます。
連立一次方程式の解法について知りたい方は線形代数学11と12の記事をご覧ください。
この記事では以下のことを紹介します。
- 一次変換とは何か
- 基本的な点の移動について
- 点の原点まわりの回転移動について
- 直線 \( y=mx \) に関する対称移動について
一次変換とは
今回は一次変換について解説していきます。
2次の正方行列 \( A \) を用いると、 \( A\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} x’ \\ y’ \end{pmatrix} \) で点 \( (x,y) \) を点 \( (x’,y’) \) に移動することができます。
この点の移動のことを一次変換といいます。
\( A=\begin{pmatrix} 3 & -2 \\ -1 & 1 \end{pmatrix} \) による一次変換を考える。
(1) 点 \( (1,2) \) がどの点に移るかを考える。
\( \begin{pmatrix} 3 & -2 \\ -1 & 1 \end{pmatrix}\begin{pmatrix} 1 \\ 2 \end{pmatrix}=\begin{pmatrix} -1 \\ 1 \end{pmatrix} \) より、点 \( (-1,1) \) に移る。
(2) どの点が点 \( (1,-1) \) に移るかを考える。
その点を \( (x,y) \) とおくと、 \( \begin{pmatrix} 3 & -2 \\ -1 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} 1 \\ -1 \end{pmatrix} \)
よって、逆行列 \( A^{-1}=\begin{pmatrix} 1 & 2 \\ 1 & 3 \end{pmatrix} \) を左からかけると、
$$ \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} 1 & 2 \\ 1 & 3 \end{pmatrix}\begin{pmatrix} 1 \\ -1 \end{pmatrix}=\begin{pmatrix} -1 \\ -2 \end{pmatrix} $$
よって、点 \( (-1,-2) \) から移る。
この例の関係を図示すると、次のようになります。
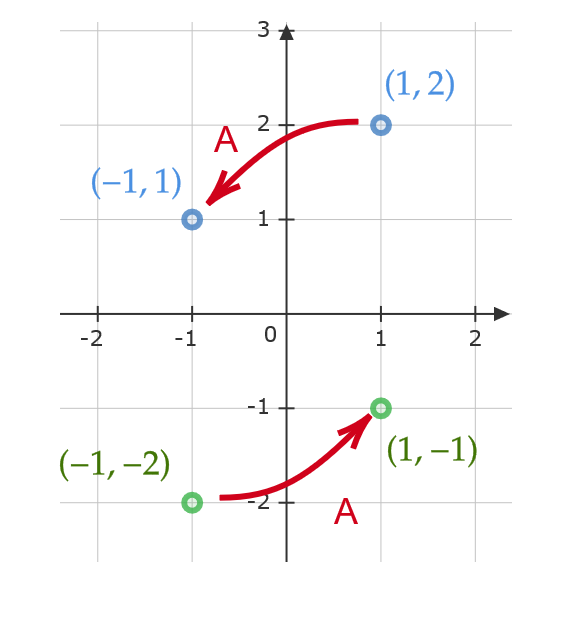
基本的な点の移動
ここでは4つの基本的な点の移動について紹介する。
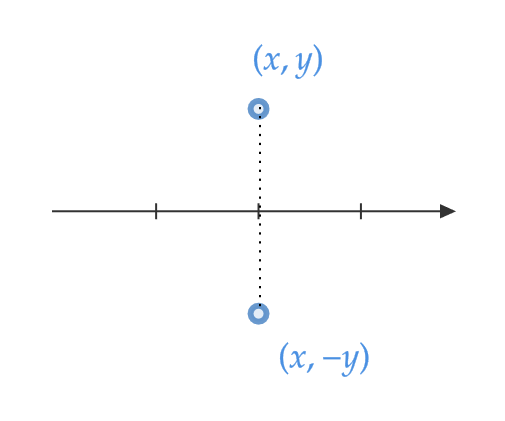
\( x \) 軸に関して対称移動
\( A=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \) とすると、図より
$$ \begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} x \\ -y \end{pmatrix} $$
となればよいということになります。
これは \( \begin{cases} ax+by=x \\ cx+dy=-y \end{cases} \) と表せます。
解くと、 \( a=1, \ b=0, \ c=0, \ d=-1 \) であるので、 \( \color{red}{A=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
} \) となります。
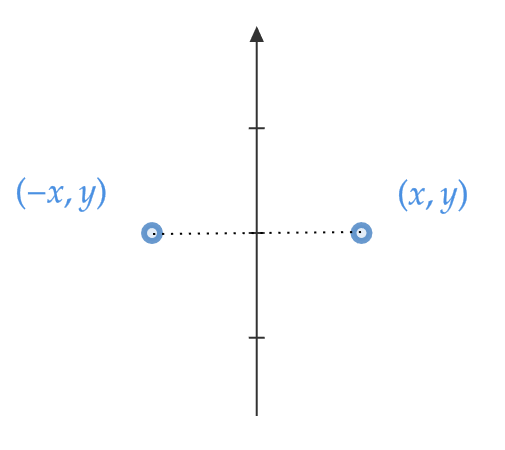
\( y \) 軸に関して対称移動
\( A=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \) とすると、図より
$$ \begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} -x \\ y \end{pmatrix} $$
となればよいということになります。
これは \( \begin{cases} ax+by=-x \\ cx+dy=y \end{cases} \) と表せます。
解くと、 \( a=-1, \ b=0, \ c=0, \ d=1 \) であるので、 \( \color{red}{A=\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}
} \) となります。
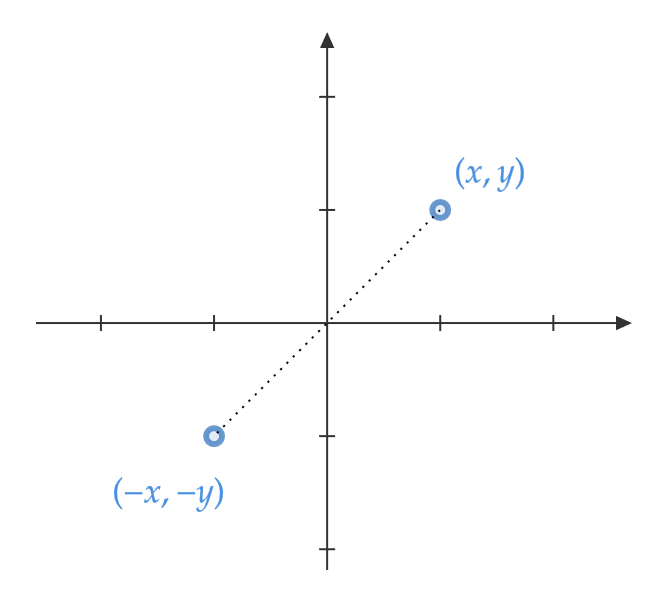
原点に関して対称移動
図より、これは \( x \) 軸に関して対称移動したあと \( y \) 軸に関して対称移動するのと同じになります。よって、
$$ \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ -y \end{pmatrix}=\begin{pmatrix} -x \\ -y \end{pmatrix} $$
(2つの行列のかける順番に注意してください)
よって、
$$ \color{red}{A}=\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\color{red}{=\begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}} $$
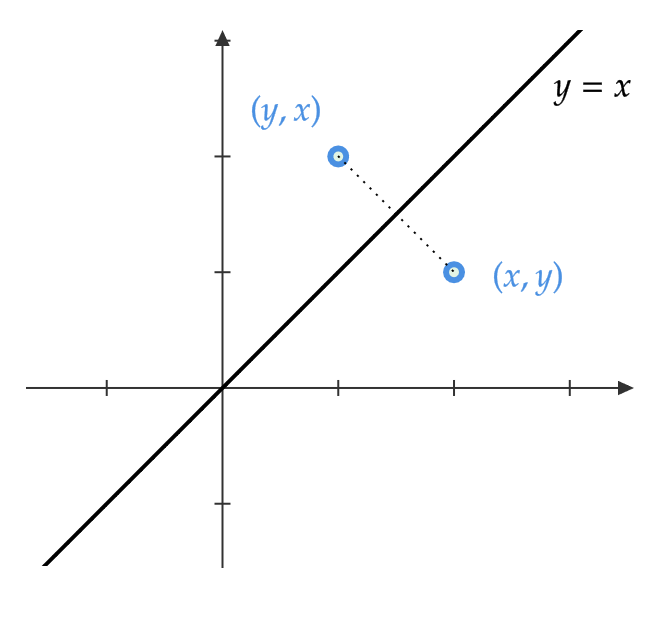
\( y=x \) に関して対称移動
\( A=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \) とすると、図より
$$ \begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} y \\ x \end{pmatrix} $$
となればよいということになります。
これは \( \begin{cases} ax+by=y \\ cx+dy=x \end{cases} \) と表せます。
解くと、 \( a=0, \ b=1, \ c=1, \ d=0 \) であるので、 \( \color{red}{A=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}
} \) となります。
点 \( (3,2) \) を \( x \) 軸に関して対称移動したあと、 \( y=x \) に関して対称移動させることを考える。
$$ \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\begin{pmatrix} 3 \\ 2 \end{pmatrix}=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} 3 \\ -2 \end{pmatrix}=\begin{pmatrix} -2 \\ 3 \end{pmatrix} $$
よって、点 \( (-2,3) \) に移る。
点の原点まわりの回転移動
点 \( (x,y) \) を原点まわりに \( \theta \) だけ回転移動する行列 \( R(\theta) \) を求めたい。
\( (x,y) \) を \( \theta \) だけ回転させた点を \( (x’,y’) \) とおきます。
\( (x,y),(x’,y’) \) をそれぞれ極座標変換して、 \( (r,\alpha),(r,\alpha+\theta) \) とおきます。
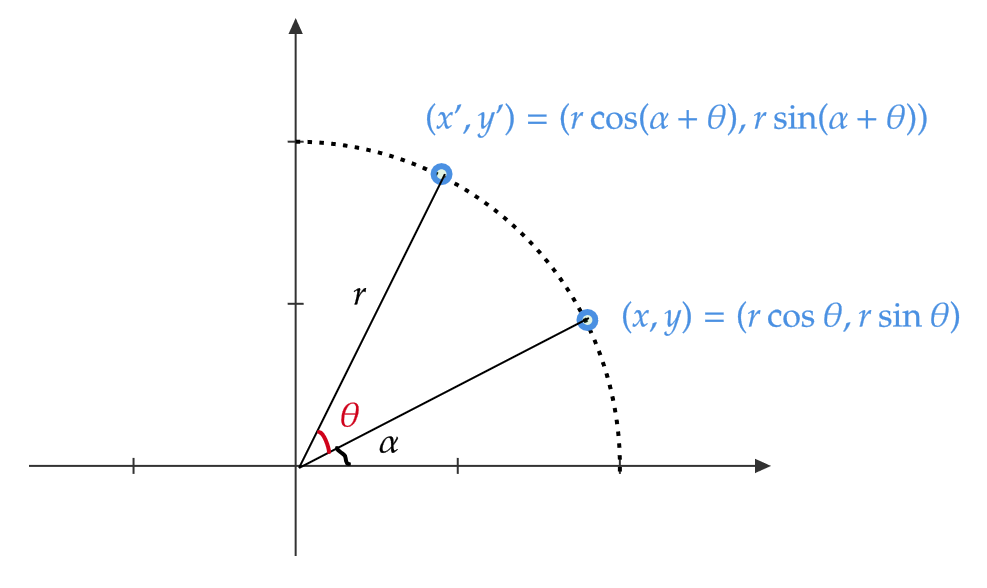
すると、
$$ \begin{align} &x=r\cos\alpha, \ y=r\sin\alpha, \\ &x’=r\cos(\alpha+\theta), \ y’=r\sin(\alpha+\theta) \end{align} $$
よって、加法定理より、
$$ \begin{align} \begin{pmatrix} x’ \\ y’ \end{pmatrix}&=\begin{pmatrix} r\cos(\alpha+\theta) \\ r\sin(\alpha+\theta) \end{pmatrix} = \begin{pmatrix} r(\cos\alpha\cos\theta-\sin\alpha\sin\theta) \\ r(\sin\alpha\cos\theta+\cos\alpha\sin\theta) \end{pmatrix} \\ &=\begin{pmatrix} \color{red}{r\cos\alpha}\cos\theta-\color{red}{r\sin\alpha}\sin\theta \\ \color{red}{r\cos\alpha}\sin\theta+\color{red}{r\sin\alpha}\cos\theta \end{pmatrix}=\begin{pmatrix} \color{red}{x}\cos\theta-\color{red}{y}\sin\theta \\ \color{red}{x}\sin\theta+\color{red}{y}\cos\theta \end{pmatrix} \\ &=\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \end{align} $$
したがって、 \( \color{red}{R(\theta)=\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}} \) となります。
点 \( (4,2) \) を原点まわりに \( \frac{2}{3}\pi \) だけ回転移動させることを考える。
\( \cos\frac{2}{3}\pi=-\frac{1}{2}, \ \sin\frac{2}{3}\pi=\frac{\sqrt{3}}{2} \) より、
$$ \begin{align} R\left(\frac{2}{3}\pi\right)\begin{pmatrix} 4 \\ 2 \end{pmatrix} &=\begin{pmatrix} \cos\frac{2}{3}\pi & -\sin\frac{2}{3}\pi \\ \sin\frac{2}{3}\pi & \cos\frac{2}{3}\pi \end{pmatrix}\begin{pmatrix} 4 \\ 2 \end{pmatrix} \\ &=\frac{1}{2}\begin{pmatrix} -1 & -\sqrt{3} \\ \sqrt{3} & -1 \end{pmatrix}\begin{pmatrix} 4 \\ 2 \end{pmatrix}=\begin{pmatrix} -1 & -\sqrt{3} \\ \sqrt{3} & -1 \end{pmatrix}\begin{pmatrix} 2 \\ 1 \end{pmatrix} \\ &=\begin{pmatrix} -2-\sqrt{3} \\ 2\sqrt{3}-1 \end{pmatrix} \end{align} $$
よって、点 \( (-2-\sqrt{3},2\sqrt{3}-1) \) に移る。
直線 \( y=mx \) に関する対称移動
\( y=x \) に限らず、一般の直線 \( y=mx \) に関して対称移動する行列を求めたい。
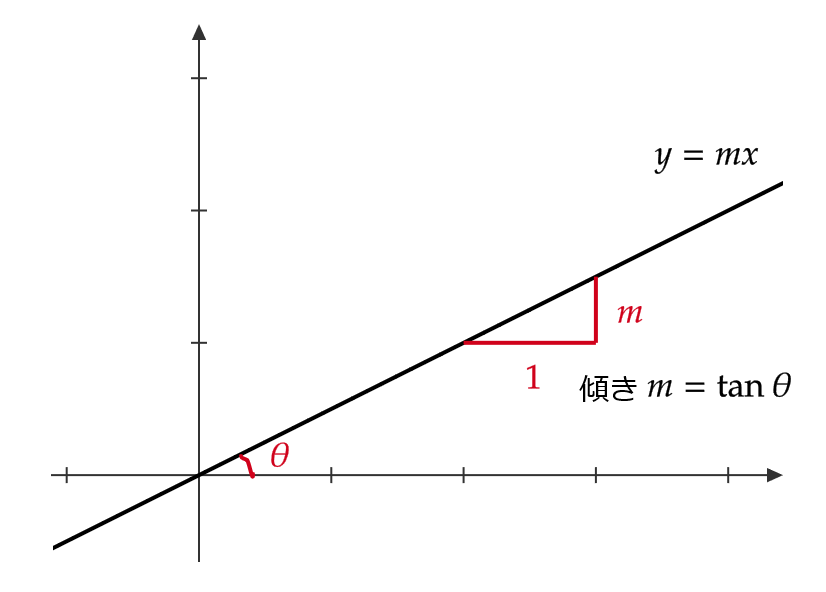
図のように \( y=mx \) の傾き \( m \) は、 \( m=\tan\theta \) で表すことができます。
よって、 \( y=(\tan\theta)\cdot x \) に関して対称移動する行列 \( T(\theta) \) を求めることにします。
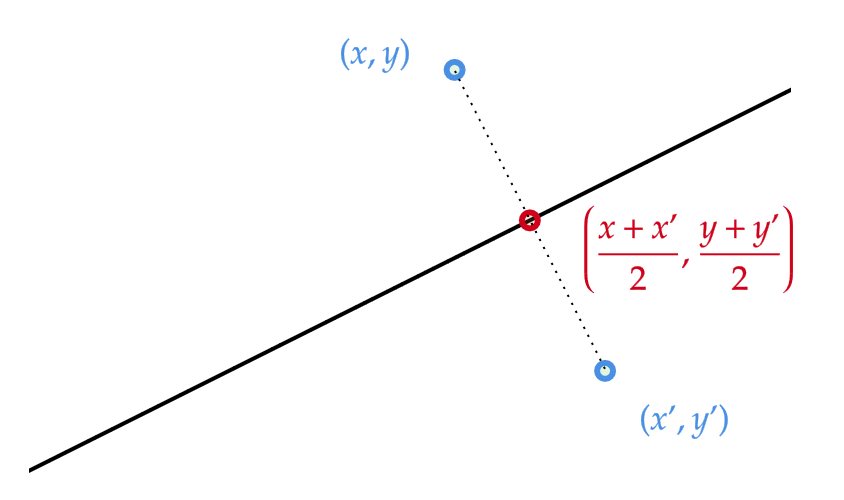
点 \( (x,y) \) が点 \( (x’,y’) \) に移るとします。
まず、2点 \( (x,y),(x’,y’) \) を端点とする線分の中点 \( \left(\frac{x+x’}{2},\frac{y+y’}{2}\right) \) は \( y=mx \) 上にあります。
よって、代入すると、 \( \frac{y+y’}{2}=m\frac{x+x’}{2} \)
したがって、
$$ mx’-y’=-mx+y \tag{1} $$
となります。
次に2点 \( (x,y),(x’,y’) \) を結ぶ直線は \( y=mx \) と直交します。
この直線を \( Y=m’X \) とおくと、 \( y=m’x, \ y’=m’x’ \) より、 \( y’-y=m'(x’-x) \) となります。
よって、この直線の傾き \( m’ \) は \( m’=\frac{y’-y}{x’-x} \)
\( y=mx \) に直交する直線の傾きは \( -\frac{1}{m} \) であるので、 \( \frac{y’-y}{x’-x}=-\frac{1}{m} \)
これを解くと、
$$ x’+my’=x+my \tag{2} $$
となります。(1),(2)を合わせると、
$$ \begin{pmatrix} m & -1 \\ 1 & m \end{pmatrix}\begin{pmatrix} x’ \\ y’ \end{pmatrix}=\begin{pmatrix} -m & 1 \\ 1 & m \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \tag{3} $$
\( \begin{vmatrix} m & -1 \\ 1 & m \end{vmatrix}=m^2+1\not=0 \) より、 \( \begin{pmatrix} m & -1 \\ 1 & m \end{pmatrix} \) は正則になります。
よって、逆行列 \( \frac{1}{m^2+1}\begin{pmatrix} m & 1 \\ -1 & m \end{pmatrix} \) を(3)の両辺に左からかけると、
$$ \begin{align} \begin{pmatrix} x’ \\ y’ \end{pmatrix}&=\frac{1}{m^2+1}\begin{pmatrix} m & 1 \\ -1 & m \end{pmatrix}\begin{pmatrix} -m & 1 \\ 1 & m \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \\ &=\frac{1}{1+m^2}\begin{pmatrix} 1-m^2 & 2m \\ 2m & -(1-m^2) \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \\ &=\begin{pmatrix} \frac{1-m^2}{1+m^2} & \frac{2m}{1+m^2} \\ \frac{2m}{1+m^2} & -\frac{1-m^2}{1+m^2} \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \end{align} $$
ここで、
$$ \begin{align} \frac{1-m^2}{1+m^2}&=\frac{1-\tan^2\theta}{1+\tan^2\theta}=\cos^2\theta\left( 1-\frac{\sin^2\theta}{\cos^2\theta} \right) \quad (1+\tan^2\theta=\frac{1}{\cos^2\theta}, \ \tan^2\theta=\frac{\sin^2\theta}{\cos^2\theta} \ \text{より}) \\ &=\cos^2\theta-\sin^2\theta=\cos2\theta \end{align} $$
$$ \begin{align} \frac{2m}{1+m^2}&=\frac{2\tan\theta}{1+\tan^2\theta}=2\cos^2\theta\cdot\frac{\sin\theta}{\cos\theta} \quad (1+\tan^2\theta=\frac{1}{\cos^2\theta}, \ \tan\theta=\frac{\sin\theta}{\cos\theta} \ \text{より}) \\ &=2\sin\theta\cos\theta=\sin2\theta \end{align} $$
したがって、
$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix}=\begin{pmatrix} \cos2\theta & \sin2\theta \\ \sin2\theta & -\cos2\theta \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} $$
よって、 \( \color{red}{T(\theta)=\begin{pmatrix} \cos2\theta & \sin2\theta \\ \sin2\theta & -\cos2\theta \end{pmatrix}} \) となります。
点 \( (2,3) \) を \( y=3x \) に関して対称移動させることを考える。
\( \tan\theta=3 \) とおくと、
$$ \cos2\theta=\frac{1-\tan^2\theta}{1+\tan^2\theta}=\frac{1-9}{1+9}=-\frac{4}{5} $$
$$ \sin2\theta=\frac{2\tan\theta}{1+\tan^2\theta}=\frac{2\times 3}{1+9}=\frac{3}{5} $$
よって、
$$ T=\begin{pmatrix} \cos2\theta & \sin2\theta \\ \sin2\theta & -\cos2\theta \end{pmatrix}=\frac{1}{5}\begin{pmatrix} -4 & 3 \\ 3 & 4 \end{pmatrix} $$
したがって、
$$ T\begin{pmatrix} 2 \\ 3 \end{pmatrix}=\frac{1}{5}\begin{pmatrix} -4 & 3 \\ 3 & 4 \end{pmatrix}\begin{pmatrix} 2 \\ 3 \end{pmatrix}=\frac{1}{5}\begin{pmatrix} 1 \\ 18 \end{pmatrix}=\begin{pmatrix} \frac{1}{5} \\ \frac{18}{5} \end{pmatrix} $$
よって、点 \( (\frac{1}{5},\frac{18}{5}) \) に移る。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

