こんにちは、ひかりです。
今回はベクトル解析から方向微分とスカラー場・ベクトル場について解説していきます。
この記事では以下のことを紹介します。
- 方向微分について
- スカラー場と等位面について
- ベクトル場と流線について
方向微分
2変数関数 \( f(x,y) \) の点 \( (a,b) \) における \( x \) に関する偏微分係数 \( f_x(a,b) \) は
\[ f_x(a,b)=\lim_{h\to0}\frac{f(a+h,b)-f(a,b)}{h} \]
で定義されていました。
これを次のように考えることもできます。
点 \( (a,b) \) を通り、単位ベクトル \( \mathbf{e}_1=(1,0) \) を方向ベクトルにもつパラメータ \( t \) の直線
\[ (x,y)=(a,b)+t(1,0)=(a+t,b) \]
を考えます。
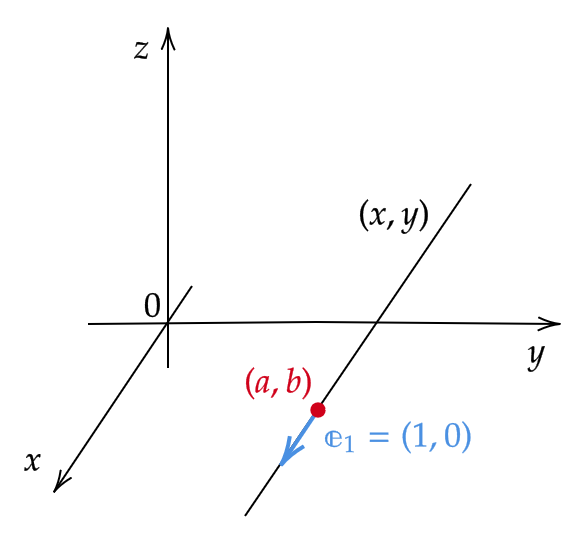
このとき、この式を \( f(x,y) \) に代入して得られる1変数関数 \( F(t)=f(a+t,b) \) は、点 \( (a,b) \) を通り \( x \) 軸に平行な直線上でのもともとの関数 \( f(x,y) \) の値を表した関数となります。
したがって、この関数 \( F(t) \) を \( t=0 \) に関して微分すると、
$$ F'(0)=\lim_{h\to 0}\frac{F(h)-F(0)}{h}=\lim_{h\to0}\frac{f(a+h,b)-f(a,b)}{h}=f_x(a,b) $$
となり、もともとの関数 \( f(x,y) \) の \( x \) に関する偏導関数と一致します。
これは言い換えると、 \( x \) 方向の偏微分というのは、単位ベクトル \( \mathbf{e}_1=(1,0) \) 方向の偏微分ということになります。
この考え方を用いると、偏微分を拡張することができます。
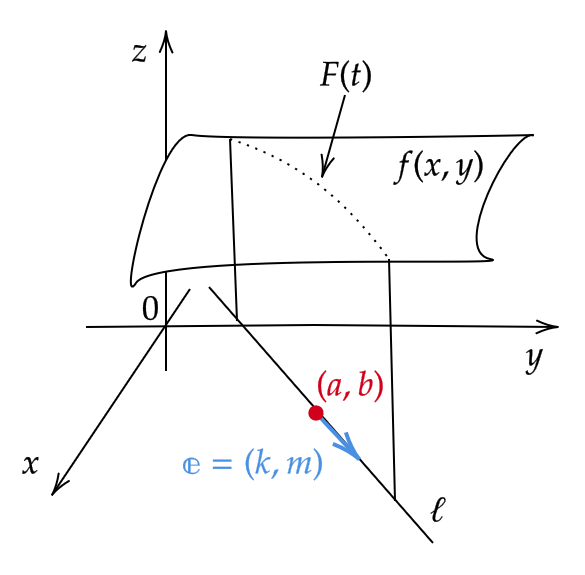
つまり、点 \( (a,b) \) を通る任意の単位ベクトル \( \mathbf{e}=(k,m) \) を方向ベクトルにもつパラメータ \( t \) の直線
\[ (x,y)=(a,b)+t(k,m)=(a+tk,b+tm) \tag{1} \]
を考えます。
このとき、この式を \( f(x,y) \) に代入して得られる1変数関数 \( F(t)=f(a+tk,b+tm) \) は、直線(1)上でのもともとの関数 \( f(x,y) \) の値を表した関数となります。
したがって、この関数 \( F(t) \) を \( t=0 \) に関して微分すると、連鎖公式より、
$$ \begin{align} F'(0)&=\frac{\partial f}{\partial x}(a,b)\frac{dx}{dt}(0)+\frac{\partial f}{\partial y}(a,b)\frac{dy}{dt}(0) \\ &=f_x(a,b)k+f_y(a,b)m \end{align} $$
よって、方向微分を次で定義します。
2変数関数 \( f(x,y) \) と単位ベクトル \( \mathbf{e}=(k,m) \) に対して、 \( f(x,y) \) の点 \( (a,b) \) における \( \mathbf{e} \)-方向微分 \( f_{\mathbf{e}}(a,b) \) を次で定義する。
$$ f_{\mathbf{e}}(a,b)=f_x(a,b)k+f_y(a,b)m $$
これは3変数以上の関数に対しても同様に定義されます。
(1) 次の2変数関数を考える。
$$ f(x,y)=x^2+xy-y^2 $$
この関数の点 \( (1,2) \) における \( \mathbf{e}=\left( \frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right) \)-方向微分を求める。
$$ f_x(x,y)=2x+y, \quad f_y(x,y)=x-2y $$
より、
$$ \begin{align} f_{\mathbf{e}}(1,2)&=f_x(1,2)\times \frac{1}{\sqrt{2}}+f_y(1,2)\times\left(-\frac{1}{\sqrt{2}}\right)=\frac{7}{\sqrt{2}} \end{align} $$
(2) 次の2変数関数を考える。
$$ f(x,y)=\begin{cases} \frac{x^2y}{x^4+y^2} & ((x,y)\not=(0,0)) \\ 0 & ((x,y)=(0,0)) \end{cases} $$
この関数は点 \( (0,0) \) において、すべての方向 \( \mathbf{e}=(k,m) \) に対して方向微分可能である。
実際、導関数の定義に従って計算をすると、まず \( \mathbf{e}=(0,1) \) のときは、
$$ \begin{align} f_{\mathbf{e}}(0,0)&=\lim_{h\to0}\frac{f(h,0)-f(0,0)}{h}=0 \end{align} $$
次に \( \mathbf{e}=(k,m), \ m\not=0 \) のときは、
$$ \begin{align} f_{\mathbf{e}}(0,0)&=\lim_{h\to0}\frac{f(hk,hm)-f(0,0)}{h} \\ &=\lim_{h\to0}\frac{1}{h}\left( \frac{(hk)^2(hm)}{(hk)^4+(hm)^2}-0\right) \\ &=\lim_{h\to0}\frac{1}{h}\left( \frac{h^3k^2m}{h^4k^4+h^2m^2}\right) \\ &=\lim_{h\to0}\frac{k^2m}{h^2k^4+m^2}=\frac{k^2m}{m^2}=\frac{k^2}{m} \end{align} $$
となるので、すべての方向 \( \mathbf{e}=(k,m) \) に対して方向微分可能である。
しかし、この関数は点 \( (0,0) \) で全微分可能ではない。(微分積分学09の例1(2)をご覧ください。)
スカラー場と等位面
ここからは、ベクトル解析において今後よく用いられるスカラー場とベクトル場について紹介していきます。
まず、スカラー場とは次のように定義されます。
ある領域 \( D \) 内のすべての点 \( P \) に対して1つスカラーが対応する場合、この領域 \( D \) のことをスカラー場という。
とくに、 \( D \) が2次元領域の場合は平面スカラー場、3次元領域の場合は空間スカラー場という。
\( D \) をスカラー場とすると、各点 \( P \) に対してその点に対応するスカラーを対応させた関数 \( f(P) \) が定まる。
この関数 \( f \) のことをスカラー場 \( D \) に対応するスカラー値関数という。
しかし、とくに混乱のおそれがない限り、この \( f \) のことをスカラー場とよぶことにする。
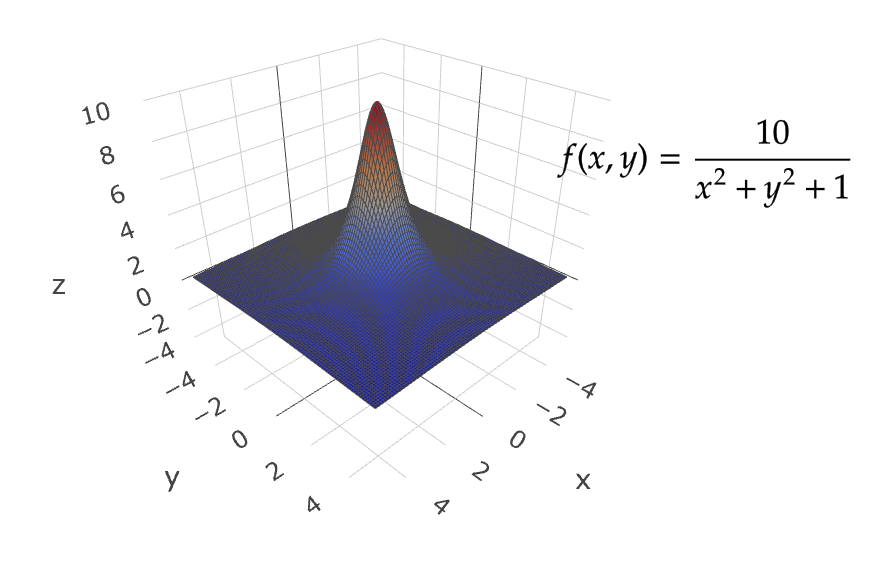
\( \mathbb{R}^2 \) 内のすべての点 \( (x,y) \) に対して、スカラーを
$$ f(x,y)=\frac{10}{x^2+y^2+1} $$
で与えられるとき、 \( \mathbb{R}^2 \) はスカラー場となる。
このとき、スカラー場 \( \mathbb{R}^2 \) に対応するスカラー値関数は \( f \) である。
グラフとしては次のようになる。
平面スカラー場には等位曲線、空間スカラー場には等位曲面というものが存在します。
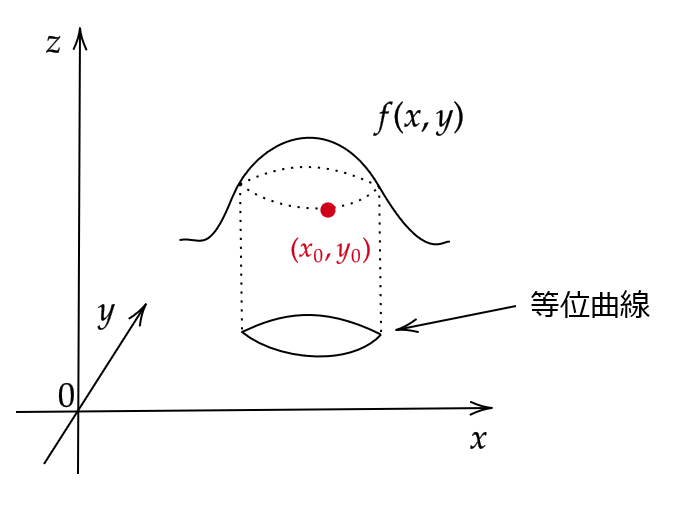
(1) 領域 \( D \) 上の平面スカラー場 \( f(x,y) \) をとる。
このとき、ある1点 \( (x_0,y_0)\in D \) に対して、
$$ f(x,y)=f(x_0,y_0) $$
となるような \( (x,y)\in D \) の集合はある曲線を表す。
この曲線のことを点 \( (x_0,y_0) \) に関する等位曲線という。
(2) 領域 \( D \) 上の空間スカラー場 \( f(x,y,z) \) をとる。
このとき、ある1点 \( (x_0,y_0,z_0)\in D \) に対して、
$$ f(x,y,z)=f(x_0,y_0,z_0) $$
となるような \( (x,y,z)\in D \) の集合はある曲面を表す。
この曲面のことを点 \( (x_0,y_0,z_0) \) に関する等位曲面という。
例2のスカラー場
$$ f(x,y)=\frac{10}{x^2+y^2+1} $$
を考える。このスカラー場の点 \( (0,-2) \) に関する等位曲線を求める。
つまり、
$$ f(x,y)=f(0,-2)=\frac{10}{5}=2 $$
をみたせばよいので、
$$ \frac{10}{x^2+y^2+1}=2 $$
したがって、等位曲線は
$$ x^2+y^2=4 $$
ベクトル場と流線
次にベクトル場について定義していきます。
ある領域 \( D \) 内のすべての点 \( P \) に対して1つベクトルが対応する場合、この領域 \( D \) のことをベクトル場という。
とくに、 \( D \) が2次元領域の場合は平面ベクトル場、3次元領域の場合は空間ベクトル場という。
\( D \) をベクトル場とすると、各点 \( P \) に対してその点に対応するベクトルを対応させたベクトル値関数 \( \mathbf{V}(P) \) が定まる。
このベクトル値関数 \( \mathbf{V} \) のことをベクトル場 \( D \) に対応するベクトル値関数という。
しかし、とくに混乱のおそれがない限り、この \( \mathbf{V} \) のことをベクトル場とよぶことにする。
\( \mathbb{R}^2 \) 内のすべての点 \( (x,y) \) に対して、ベクトルを
$$ \mathbf{V}(x,y)=(-y,x) $$
で与えられるとき、 \( \mathbb{R}^2 \) はベクトル場となる。
このとき、ベクトル場 \( \mathbb{R}^2 \) に対応するベクトル値関数は \( \mathbf{V} \) である。
グラフとしては次のようになる。
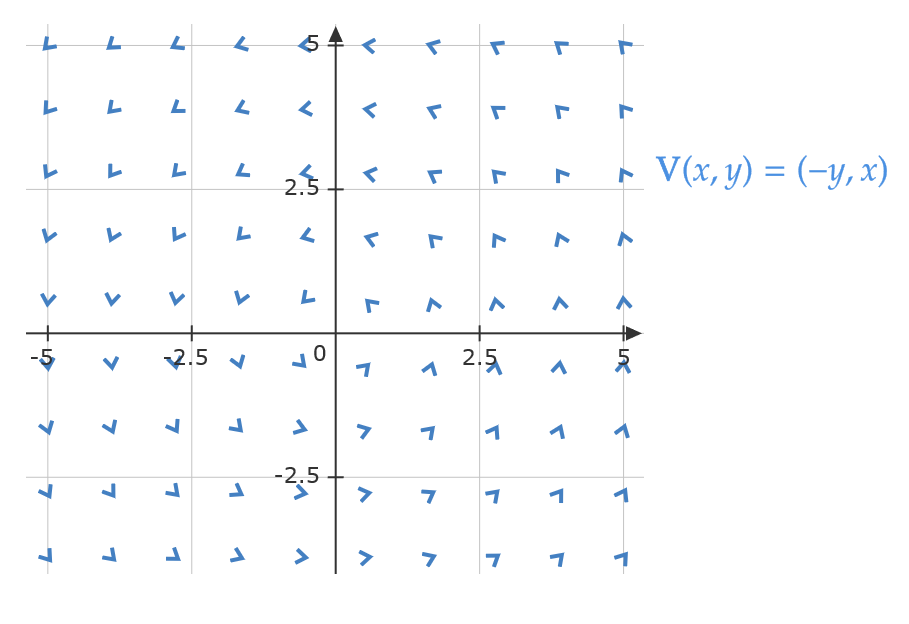
ベクトル場には流線というものが存在します。
領域 \( D \) 上の空間スカラー場
$$ \mathbf{V}(x,y,z)=(f(x,y,z),g(x,y,z),h(x,y,z)) $$
をとる。このとき、 \( D \) 上で定義される微分方程式
$$ \frac{d\mathbf{r}}{dt}=\mathbf{V}(\mathbf{r}), \quad \mathbf{r}=(x,y,z)\in D $$
すなわち、
$$ \frac{dx}{dt}=f(x,y,z), \quad \frac{dy}{dt}=g(x,y,z), \quad \frac{dz}{dt}=h(x,y,z) $$
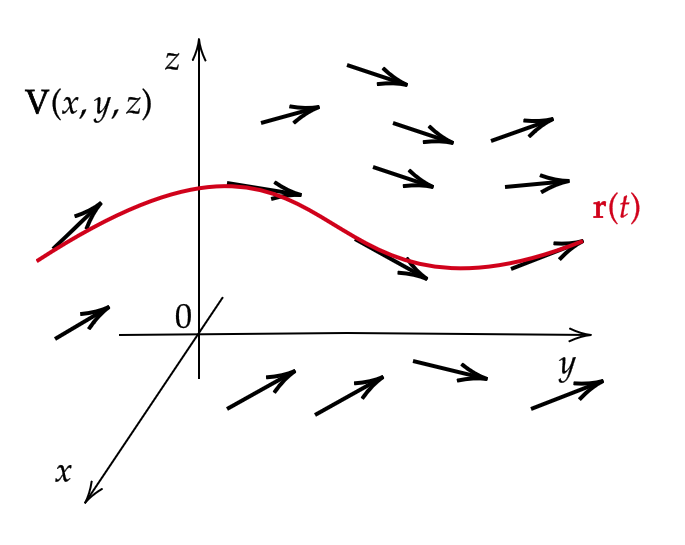
の解で与えられる \( D \) 上の曲線 \( \mathbf{r}=\mathbf{r}(t) \) をベクトル場 \( \mathbf{V} \) の流線という。
流線のイメージは次のようである。
例4のベクトル場
$$ \mathbf{V}(x,y)=(-y,x) $$
を考える。このベクトル場の流線を求める。
つまり、
$$ \frac{dx}{dt}=-y, \quad \frac{dy}{dt}=x $$
をみたせばよいので、
$$ \frac{dx}{-y}=\frac{dy}{x} $$
したがって、この微分方程式は変数分離形であるので、これを解くと、
$$ x^2+y^2=C^2 \quad (C:任意) $$
となるので、流線は原点 \( O \) を中心とする同心円群である。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

